Kezdőlap


Feladat:	608. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Kótai Endre , Takács László
Füzet:	1966/december, 237 - 238. oldal		PDF \| MathML
Témakör(ök):	Egyenletesen gyorsuló rendszerek, Erők forgatónyomatéka, Lejtő, Tapadó súrlódás, Feladat
Hivatkozás(ok):	Feladatok: 1966/május: 608. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A megadott $P$ húzóerő ellen a súlyerő $P_{m}$ lejtőirányú összetevője és a $P_{s}$ súrlódási erő hat. A mozgásegyenlet tehát

\begin{matrix} (m_{1} & + m_{2}) a = P - P_{m} - P_{s}, így \\ a & = \frac{P}{m_{1} + m_{2}} - g (sin α + cos α) . \end{matrix}

A számadatokat beírva (

P = 10, 866 \cdot g N

)

\begin{matrix} a = g / 2. \end{matrix}

A kúp a hasábbal együtt

g / 2

gyorsulással mozog, ezért a ráható tehetetlenségi erő a mozgással ellentétes irányban

\begin{matrix} P_{t} = m_{kúp} \cdot a = 2 kp. \end{matrix}

A kúp egyensúlyi helyzete attól függ, hogy a

P_{t}

tehetetlenségi és a

G

súlyerő eredője a kúp alaplapján áthalad-e vagy sem. A két erő adott, tehát az eredő iránya meghatározott. Az egyensúlyi helyzet így csak a kúp magasságvonalában levő súlypont (és tömegközéppont) helyzetétől függ.
A kúp súlya adott, ezért térfogata, illetve magassága a fajsúlyától függ:

\begin{matrix} γ = G / V = \frac{G}{R^{2} π h / 3} . \end{matrix}

A súlypont a kúp magasságvonalának alsó negyedében van (bizonyítás a megjegyzésben), ezért a súlypont helyzete és a fajsúly között egyértelmű és fordítottan arányos összefüggés van.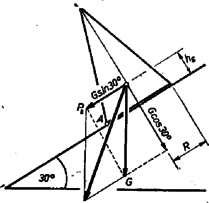

\begin{matrix} h_{s} = h / 4 = 3 G / 4 R^{2} π \cdot γ . \end{matrix}

Nyilvánvaló, hogy csak a labilis egyensúlyi helyzetet kell meghatároznunk, amely trigonometriai megfontolások alapján adódik.

1. ábra

Egyszerűbb az egyensúlyi viszonyok meghatározása, ha a kúp legalsó (

A

) pontjára felírjuk az erők forgatónyomatékát (1. 1. ábra). A súlyerőt felbontva a lejtővel párhuzamosan hat

P_{t} + G \cdot sin 30^{\circ}

, a lejtőre merőlegesen

G \cdot cos 30^{\circ}

. A megfelelő erőkarok

h / 4

, ill.

R

. Így

\begin{matrix} M = (P_{t} + G \cdot sin 30^{\circ}) \frac{h}{4} - G \cdot cos 30^{\circ} \cdot R . \end{matrix}

M < 0

, az egyensúly stabil, ha

M > 0

, a kúp ledől.
Az

M = 0

határesetben az egyensúly labilis. Az előbbiek szerint ekkor a magasság

h = 17, 32 cm

és a fajsúly

γ = 8, 82 {p/cm}^{3}

. Ha a fajsúly ennél az értéknél nagyobb, a súlypont alacsonyabbra kerül (az alaplaphoz viszonyítva), ekkor a kúp helyzete stabil, ha a fajsúly kisebb, akkor a kúp ledől.

Kótai Endre (Bp., Apáczai Cs. J. g. II. o. t.)

Takács László (Sopron; Széchenyi I. g. II. o. t.)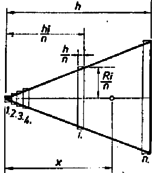

2. ábra

Megjegyzés. A homogén forgáskúp súlypontjának meghatározása: Helyezzük el a kúpot úgy, hogy magasságvonala vízszintes legyen. Osszuk a magasságvonalra merőleges síkokkal

n

egyenlő vastagságú részre (1. 2. ábra). Ha

n

elég nagy, akkor az osztás során létrejött csonkakúpok helyettesíthetők ugyanolyan magas hengerekkel, amelyek sugara az alapkörök sugarával egyezik meg. Az egyes hengerek magassága

h / n

. Írjuk fel a súlyerők forgatónyomatékát a kúp csúcsára vonatkoztatva. A súlypontban ható eredő súly forgatónyomatéka egyenlő lesz a felosztott kúprészek forgatónyomatékainak összegével. A számozást a csúcsból kezdve az

i .

henger alapjának távolsága a csúcsból

h \cdot i / n

és sugara

R \cdot i / n

. Így forgatónyomatéka

\begin{matrix} M_{i} = V_{I} \cdot γ (h \cdot i / n) = {(R i / n)}^{2} \cdot π \cdot (h / n) \cdot γ \cdot (h \cdot i / n) = R^{2} \cdot π \cdot γ \cdot \frac{h^{2}}{n^{4}} i^{3} . \end{matrix}

Ezeket a forgatónyomatékokat az összes

n

-re összegezve kapjuk az eredőt.

\begin{matrix} M_{e} = R^{2} \cdot π \cdot h \cdot γ \cdot x / 3 = \sum_{l = 1}^{n} R^{2} \cdot π \cdot γ \cdot \frac{h^{2}}{n^{4}} \cdot i^{3}, \end{matrix}

ahol

x

a súlypont távolsága a csúcsból. Az állandókat kiemelve és egyszerűsítve

\begin{matrix} x / 3 = h / n^{4} \cdot \sum_{i = 1}^{n} i^{3} . \end{matrix}

Belátható, hogy az első

n

köbszám összege

\begin{matrix} 1^{3} + 2^{3} + ... + n^{3} = \sum_{i = 2}^{n} i^{3} = {[\frac{n (n + 1)}{2}]}^{2}, \end{matrix}

ezt az előbbi kifejezésbe írva

\begin{matrix} x / 3 = h / n^{4} \cdot {[\frac{n (n + 1)}{2}]}^{2} . \end{matrix}

n

-et egyre növeljük, a hengerek egyre jobban közelítik a kúpot, a kifejezésben pedig

a + 1

összeadandó elhanyagolható lesz

n

mellett, így mondhatjuk, hogy nagy

n

esetén

\begin{matrix} \frac{x}{3} \approx \frac{h}{n^{4}} \cdot \frac{n^{4}}{4} = \frac{h}{4}, amiből \end{matrix}

x = 3 h / 4

, amint azt bizonyítani kívántuk.

Takács László (Sopron, Széchenyi I. g. II. o. t.)