Kezdőlap


Feladat:	578. fizika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bucsy Péter , Fogaras András , Marossy Ferenc , Szeidl László
Füzet:	1966/szeptember, 38 - 40. oldal		PDF \| MathML
Témakör(ök):	Coulomb-törvény, Coulomb-potenciál, Coulomb-energia, Tömegpont egyensúlya, Közelítő számítások, numerikus módszerek, Feladat
Hivatkozás(ok):	Feladatok: 1966/január: 578. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Tételezzük fel, hogy a golyót csak igen lassan engedjük mozogni. Ebben az esetben centrifugális erő nem lép fel. $Q_{2}$ helyzetét az $α$ középponti szöggel jellemezzük (1. ábra). $Q_{2}$ -re három erő hat: az elektromos taszítóerő, a súlyerő és a sugárirányú kényszererő, amely azt biztosítja, hogy a gömbön maradjon. Tételezzük fel először azt, hogy a kényszererő előjele tetszés szerinti lehet, vagyis a $Q_{2}$ töltés a gömbbe sem behatolni, sem pedig róla lerepülni nem tud. Vizsgáljuk meg, hol lesz a bodzabélgolyó egyensúlyban!

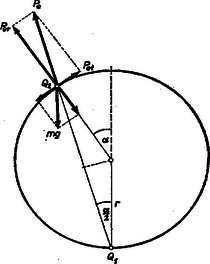1. ábra

Az egyensúlyi helyzet megállapításához fel kell írni a

Q_{2}

-re ható tangenciális erőket mint

α

szög függvényét. Az elektromos taszítóerő:

\begin{matrix} P_{e} = \frac{k Q_{1} Q_{2}}{4 r^{2} cos^{2} \frac{α}{2}} . \end{matrix}

Ennek tangenciális összetevője:

\begin{matrix} P_{et} = P_{e} sin \frac{α}{2} = \frac{k Q_{1} Q_{2} sin \frac{α}{2}}{4 r^{2} cos^{2} \frac{α}{2}} . \end{matrix}

(1)

m g

súlyerő tangenciális összetevője

m g sin α

, ezért az eredő tangenciális erő ‐ felfelé számítva a pozitív irányt:

\begin{matrix} P_{t} = \frac{k Q_{1} Q_{2} sin \frac{α}{2}}{4 r^{2} cos^{2} \frac{α}{2}} - m g sin α & = 2 sin \frac{α}{2} (\frac{k Q_{1} Q_{2}}{8 r^{2} cos^{2} \frac{α}{2}} - m g cos \frac{α}{2}) . & (2) \end{matrix}

Az egyensúly feltétele, hogy ez nulla legyen. Szorzatról lévén szó, az egyik megoldás:

sin \frac{α}{2} = 0

, azaz

α = 0

. Ez a gömb tetején levő egyensúlyi helyzetet jelenti. A másik tényezőt egyenlővé téve 0-val kapjuk, hogy

\begin{matrix} cos \frac{α}{2} = \sqrt[3]{\frac{k Q_{1} Q_{2}}{8 r^{2} m g}} . \end{matrix}

(3)

Ennek az egyenletnek csak akkor van fizikailag használható megoldása, ha a jobb oldal nemnegatív és nem nagyobb 1-nél. (3) jobb oldala csak akkor lehet nulla, ha nincs elektromos erő jelen és ekkor

α = 180^{\circ}

Q_{2}

lenn marad. Ezután három esetet különböztetünk meg.
a) Ha

k Q_{1} Q_{2} / 8 r^{2} < m g

, akkor két egyensúlyi helyzet van, az egyik a gömb tetején, a másik a (3) által megadott helyen.
b) Ha

k Q_{1} Q_{2} / 8 r^{2} = m g

, akkor a két egyensúlyi helyzet egybeesik a gömb tetején.
c) Ha

k Q_{1} Q_{2} / 8 r^{2} > m g

, akkor már csak a gömb tetején levő egyensúlyi helyzet valósul meg.
A feladatunk adatai szerint az erőt dinben számítva

k = 9 \cdot 10^{18}

, és azonnal látjuk, hogy (3) baloldala 540 din, a bodzabélgolyócska súlya 1125 din, tehát a) eset valósul meg. Behelyettesítve számadatainkat

cos \frac{α}{2} = 0, 7830

\frac{α}{2} = 38^{\circ} 27'

α = 76^{\circ} 54'

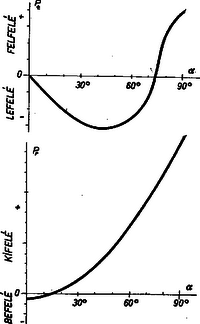2. ábra

Meg kell még vizsgálnunk az egyensúlyi helyzetek stabilitását. Felrajzoljuk a teljes

P_{t}

tangenciális erőt (2) szerint mint

α

függvényét (2. ábra felső rajza). A felfelé vivő erőt vesszük pozitívnak. A gömb tetején levő egyensúlyi helyzet labilis, hiszen a bodzabélgolyót kimozdítva az

α = 0

-hoz tartozó helyzetből lefelé ható tangenciális erőt kapunk, amely a golyócskát még inkább lefelé viszi. A

76^{\circ} 54'

-hez tartozó egyensúlyi helyzet stabilis, mert

α

-t csökkentve lefelé,

α

-t növelve felfelé ható tangenciális erőt kapunk, amely a golyócskát visszaviszi egyensúlyi helyzetébe.
De felmerül még egy probléma. Vizsgáljuk meg a teljes rádiusz mentén ható erőt:

\begin{matrix} P_{r} = \frac{k Q_{1} Q_{2}}{4 r^{2} cos \frac{α}{2}} - m g cos α . \end{matrix}

(4)

A 2. ábra alsó rajza

P_{r}

-nek

α

-tól való függését mutatja. A görbéből látjuk, hogy a radiális erő csak

α = 14^{\circ} 36'

-ig mutat befelé, azután kifelé mutat. Ha a gömb külső felületére helyezzük a bodzabélgolyót, akkor már ezen a helyen lerepül, mielőtt elérné az

α = 76^{\circ} 54'

-hez tartozó stabilis egyensúlyi helyzetet. Tehát ha a bodzabélgolyót a gömb tetejéről szép lassan lefelé tologatjuk, akkor

α = 14^{\circ} 36'

-nél át kell helyeznünk a gömb belső felületére, ha nem akarjuk, hogy lerepüljön a golyó felszínéről.

Marossy Ferenc (Bp., Fazekas g. II. o. t.) dolgozata alapján

II. megoldás. A feladat szövegezése lehetővé tette azt, hogy a bodzabélgolyó gyors mozgását feltételezve a centrifugális erőt is figyelembe vegyük. A golyót kimozdítjuk felső labilis egyensúlyi helyzetéből és meg akarjuk keresni, mikor hagyja el a gömb felszínét. Világos, hogy ez a szög kisebb lesz, mint az első megoldásban kapott eredmény, mert most a centrifugális erő is segíti a lerepülést. Legyen

v

a golyó kerületi sebessége, akkor a centrifugális erő

m v^{2} / r

és irány szerint radiálisan kifelé mutat. Az így módosított (4) szerinti radiális erőt tesszük egyenlővé 0-val:

\begin{matrix} P_{r} = \frac{k Q_{1} Q_{2}}{4 r^{2} cos \frac{α}{2}} - m g cos α + \frac{m v^{2}}{r} = 0. \end{matrix}

(

4'

)

Ki kell fejeznünk

v

sebességet

α

-val. Ezt az energiatétel felhasználásával tehetjük meg. Ismeretes, hogy egy

Q_{2}

pontszerű töltés potenciálja egy

Q_{1}

töltéstől

x

távolságra:

\begin{matrix} U = \frac{k Q_{1} Q_{2}}{x} . \end{matrix}

(Lásd pl. Kugler S.-Kugler S.-né Fizikai képletek és táblázatok 172. oldal.)
Ezt felhasználva

Q_{2}

energiája tetszőleges

α

szögnél:

\begin{matrix} E = m g r (1 + cos α) + \frac{k Q_{1} Q_{2}}{2 r cos \frac{α}{2}} + \frac{m v^{2}}{2} . \end{matrix}

(5)

Tudjuk, hogy a gömb tetején a golyócska áll, tehát

α = 0

-nál

v = 0

. Ezt (5)-be helyettesítve megkapjuk a teljes energiát, majd az energiamegmaradás alapján ez érvényes tetszőleges

α

esetére is. Eredményünket (5) baloldalába írva a kapott egyenletből kifejezzük

v^{2}

-et:

\begin{matrix} v^{2} = 2 g r (1 - cos α) + \frac{k Q_{1} Q_{2}}{m r} (1 - \frac{1}{cos \frac{α}{2}}) . \end{matrix}

Ezt behelyettesítve

(4')

-be olyan egyenletet kapunk, amelyben már csak

α

az ismeretlen. Rendezés után ez az egyenlet a következő alakot ölti:

\begin{matrix} 24 m g cos^{3} \frac{α}{2} - (20 m g + \frac{4 k Q_{1} Q_{2}}{r^{2}}) cos \frac{α}{2} + \frac{3 k Q_{1} Q_{2}}{r^{2}} = 0. \end{matrix}

Ezt az egyenletet közelítő módszerrel megoldva (

g

pontos értékét használva) az eredmény

α = 6^{\circ} 48'

. Ennél a szögnél repül le a gömb külső felületéről a bodzabélgolyó és további egyensúlyi helyzetet így már nem képes felvenni.

Szeidl László (Bp., Apáczai g. IV. o. t.) dolgozata alapján

Megjegyzések. A dolgozatok elbírálása során egyforma értékűnek fogadtuk el a centrifugális erővel vagy anélkül végzett számításokat, valamint olyant is, amely

Q_{1}

mozgását is lehetőnek képzelte. Az egyensúlyi helyzetet számítással úgy határozhatjuk meg, hogy az egyensúlyi helyzet környezetében levő szöget felírjuk, mint az egyensúlyi szög és egy kis szög összegét. Az eredmény igen érzékeny

g

számértékére, például pontos

g

-vel számolva az egyensúlyi helyzet

75^{\circ} 41'

-nek, a lerepülési szög (centrifugális erő nélkül számítva)

9^{\circ} 12'

-nek adódik.