Kezdőlap


Feladat:	570. fizika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Nagy Dénes Lajos
Füzet:	1966/április, 189 - 192. oldal		PDF \| MathML
Témakör(ök):	Mágneses térerősség (H), Körvezető mágneses tere, Egyéb áram mágneses tere, Feladat
Hivatkozás(ok):	Feladatok: 1965/december: 570. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feladat szövege félreértésre adott lehetőséget, továbbá a megoldáshoz szükséges összefüggés sem állt mindenkinek rendelkezésre. A beérkezett 31 dolgozat egyike sem tartalmazott helyes megoldást. Ezért a feladatot nem pontozzuk. Itt közöljük a pontos szöveget és a megoldást. A felhasznált összefüggéssel foglalkozik még a lapunk 178. oldalán közölt cikk.

Egy

R

sugarú fagömböt vékony dróttal tekercseljünk körül úgy, hogy az összes tekercsmenetek egymással párhuzamosak legyenek. A tekercsmenetek szorosan egymás mellett feküsznek, s egy rétegben fedik be az ábrán látható módon a gömbfelület felét. A drótban

I

erősségű áram folyik, a menetek száma

N

. Határozzuk meg a gömb középpontjában a mágneses térerősséget, tudva azt, hogy egy

r

sugarú,

I

erősségű köráram

a

síkjára a kör középpontjában emelt merőlegesen

x

távolságra

\begin{matrix} \frac{1}{2} \frac{I r^{2}}{{(x^{2} + r^{2})}^{3 / 2}} \end{matrix}

nagyságú, a síkra merőleges irányú mágneses teret hoz létre. (Ez az összefüggés akkor érvényes, ha az áramerősséget A-ban, a távolságot m-ben, a mágneses térerősséget pedig A/m-ben mérjük.)
Avégett, hogy az összes menetektől származó térerősséget kiszámítsuk, osszuk fel az első negyedet

n

egyenlő,

Δ φ

nagyságú szögre. Az osztópontok tehát

\begin{matrix} 0, Δ φ, 2 Δ φ, ..., k Δ φ, ..., n Δ φ = \frac{π}{2} . \end{matrix}

(1)

(Megjegyezzük, hogy a szöget mindig radiánban adjuk meg.) A

k

-adik szögtartomány határpontjai eszerint:

\begin{matrix} (k - 1) Δ φ és k Δ φ . \end{matrix}

Mivel a menetek szorosan illeszkednek egymáshoz, azért bármelyik szögtartományban a menetek száma

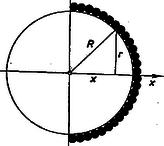\begin{matrix} Δ N = \frac{2 N}{π} Δ φ . \end{matrix}

(2)

1. ábra

Az egy menet által a középpontban létesített térerősség ‐ az 1. ábra jelöléseit használva

\begin{matrix} \frac{1}{2} \frac{I r^{2}}{{(x^{2} + r^{2})}^{3 / 2}} . \end{matrix}

(3)

Relative is kis hibát követünk el akkor, ha a menetet az

x

-tengelyhez viszonyítva jellemző szöget egy szögtartományon belül állandónak tekintjük, amennyiben

Δ φ

elég kicsi (vagyis

n

elég nagy).
Választhatjuk pl. a szögtartományt felező szöget, tehát a

k

-adik tartomány esetében ez az állandó szög:

\begin{matrix} φ_{k} = (k - \frac{1}{2}) Δ φ . \end{matrix}

(4)

Ezek alapján a

k

-adik tartomány meneteitől származó térerősséget úgy állítjuk elő mint

Δ N

db olyan menettől származó teret, amelyet a

φ_{k}

szög jellemez. Ez a térerősség:

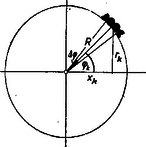\begin{matrix} Δ H_{k} = \frac{1}{2} \frac{I r^{2}}{{(x_{k}^{2} + r_{k}^{2})}^{3 / 2}} Δ N . \end{matrix}

(5)

2. ábra

Felhasználva egyrészt

Δ N

kifejezést (2), másrészt a 2. ábráról leolvasható

x_{k}^{2} + r_{k}^{3} = R^{2}

egyenlőséget, kapjuk:

\begin{matrix} Δ H_{k} = \frac{I N r_{k}^{2}}{R^{3} π} Δ φ . \end{matrix}

(6)

Mivel azonban a 2. ábra szerint

r_{k} = R sin φ_{k}

, ezért

\begin{matrix} Δ H_{k} = \frac{I N}{R π} Δ φ sin^{2} φ_{k} . \end{matrix}

(7)

A teljes térerősséget úgy kapjuk, hogy

Δ H_{k}

-t valamennyi tartományra összegezzük:

\begin{matrix} H = \sum_{k = 1}^{n} Δ H_{k} = \frac{I N}{R π} Δ φ \sum_{k = 1}^{n} sin^{2} φ_{k} . \end{matrix}

(8)

Mivel

sin^{2} α = \frac{1 - cos 2 α}{2}

, azért

\begin{matrix} \sum_{k = 1}^{n} sin^{2} φ_{k} = \sum_{k = 1}^{n} \frac{1}{2} - \sum_{k = 1}^{n} \frac{1}{2} cos 2 φ_{k} = \frac{n}{2} - \frac{1}{2} \sum_{k = 1}^{n} cos 2 φ_{k} . \end{matrix}

(9)

A továbbiakban csak a

\sum_{k = 1}^{k} cos 2 φ_{k}

meghatározásával foglalkozunk. Ez ‐ beírva

φ_{k}

(4) alatti kifejezését ‐ így alakul:

\begin{matrix} \sum_{k = 1}^{n} cos (2 k - 1) Δ φ . \end{matrix}

(10)

Legyen először

n

páros. Ekkor

n / 2

egész, tehát ez a szumma így írható:

\begin{matrix} \sum_{k = 1}^{n / 2} cos (2 k - 1) Δ φ + \sum_{k = n / 2 + 1}^{n} cos (2 k - 1) Δ φ . \end{matrix}

(11)

A második tagban felhasználjuk, hogy

cos α = - cos (π - α)

, ezért

cos (2 k - 1) Δ φ = - cos [π - (2 k - 1) Δ φ]

. De (1) szerint

π = 2 n Δ φ

, tehát ez így írható tovább:

- cos [2 (n - k) + 1] Δ φ = - cos (2 k' - 1) Δ φ

, ahol

k'

-vel az

n - k + 1

egész számot jelöltük.
Milyen értékeket vesz fel

k'

, miközben

k

végigfut

(n / 2 + 1)

-től

n

-ig ? Világos, hogy ezalatt

k'

n / 2

-től

1

-ig fut, tehát a második tag így alakul:

\begin{matrix} \sum_{k = n / 2 + 1}^{n} cos (2 k - 1) Δ φ = - \sum_{k' = 1}^{n / 2} cos (2 k' - 1) Δ φ . \end{matrix}

(12)

Látható, hogy ‐ mivel az összegező index jelölésének nincs jelentősége (11)-ben az első és a második tag kiesik. Ezért

n

páros értékeire

\begin{matrix} \sum_{k = 1}^{n} cos (2 k - 1) Δ φ = 0. \end{matrix}

(13)

n

páratlan, akkor

(\frac{n}{2} - \frac{1}{2})

(\frac{n}{2} + \frac{1}{2})

és

(\frac{n}{2} + \frac{3}{2})

egymást követő egész számok. Ezért ekkor a szumma így írható:

\begin{matrix} \sum_{k = 1}^{\frac{n}{2} - \frac{1}{2}} cos (2 k - 1) Δ φ + cos [2 (\frac{n}{2} + \frac{1}{2}) - 1] Δ φ + \sum_{k = \frac{n}{2} + \frac{3}{2}}^{n} cos (2 k - 1) Δ φ . \end{matrix}

(14)

A középső tagról azonnal látjuk, hogy eltűnik, mert a szögletes zárójelben

n

áll,

n Δ φ = \frac{π}{2}

, és

cos \frac{π}{2} = 0

. A második szummát most is könnyen átalakíthatjuk, és

k' = n + k - 1

jelöléssel az előző esethez hasonlóan, az első szummától csak előjelben és az összegező index jelölésében fog eltérni. Ezért páratlan

n

-re is:

\begin{matrix} \sum_{k = 1}^{n} cos (2 k - 1) Δ φ = 0. \end{matrix}

(15)

Most már a célnál vagyunk: eredményünk szerint

\begin{matrix} \sum_{n = 1}^{n} sin^{2} φ_{k} = \frac{n}{2} . \end{matrix}

(16)

Ezt a teljes térerősség (8) kifejezésébe helyettesítve:

\begin{matrix} H = \frac{I N n Δ φ}{2 R π} . \end{matrix}

(17)

Felhasználva, hogy

n Δ φ = \frac{π}{2}

, kapjuk, hogy közelítőleg

\begin{matrix} H = \frac{I N}{4 R} . \end{matrix}

(18)

Nagy Dénes Lajos