Kezdőlap


Feladat:	545. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Agárdy Gyula , Grosz Tamás , Horváth Sándor , Marossy Ferenc , Mihály László , Pap Márta , Takács László
Füzet:	1966/február, 91 - 92. oldal		PDF \| MathML
Témakör(ök):	Egyéb síkmozgás, Tömegpont egyensúlya, Nyomóerő, kötélerő, Feladat
Hivatkozás(ok):	Feladatok: 1965/október: 545. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feladat feltételeiből látható, hogy a csiga a kötélen gördülve egy ellipszisen halad, amelynek fókuszpontjai a felfüggesztési pontok. (Az ellipszis mindazon pontok mértani helye, amelyek két meghatározott ponttól való távolságainak összege állandó.) Azt is tudjuk, hogy egy kényszerpályán mozgó test akkor lesz nyugalomban, ha energiája minimális, és ez jelen esetben az ellipszis legmélyebb pontja. E pont meghatározása többféleképpen lehetséges.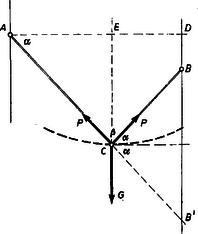

1. Az ellipszis legmélyebb pontján az érintő vízszintes. Ugyanis adott pontban az ellipszis érintője az az egyenes, amelynek pontosan egy közös pontja van az ellipszissel. A legmélyebben fekvő pont esetében a vízszintes egyenes nyilván ilyen tulajdonságú, hiszen ellenkező esetben, ha lenne ennek az ellipszissel két közös pontja, akkor lenne az ellipszisnek még mélyebben fekvő pontja. ‐ Az ellipszis érintője az érintési ponthoz húzott két vezéregyenessel azonos szöget zár be. Tehát a csigától jobbra és balra fekvő kötéldarabok is a vízszintessel egyenlő szöget zárnak be.

2. A csiga a kötélen csak egy helyen van nyugalomban. Ha a kötélszáraknak a vízszintessel való hajlásszöge egyenlő, akkor nyugalomban van. (Ebben az esetben ugyanis a kötélben fellépő húzóerők és azok vízszintes összetevői is egyenlők, így a testre ható erők eredője nulla.)
A fenti két állításból következik, hogy a csiga akkor és csak akkor van nyugalomban, ha a kötélszárak vízszintessel bezárt hajlásszöge egyenlő.
A feltételekből már könnyű a csiga helyzetét meghatározni. Tükrözzük az alacsonyabban rögzített kötéldarabot a nyugalmi pontra fektetett vízszintes egyenesen. A keletkezett háromszögekben

A D = 10 m

A B' = 15 m

B D = 2 m

, továbbá a háromszögekből leolvasható, hogy

\begin{matrix} cos α = A D / A B', α = {48, 2}^{\circ}, \\ \bar{A E} : \bar{C E} = \bar{A D} : \bar{D B'}, \\ \bar{C E} = 2 + \frac{1}{2} (\bar{B' D} - 2) = 1 + \bar{B' D} / 2. \end{matrix}

A két utóbbi egyenletből

\begin{matrix} \bar{A E} = 5, 89 m . \end{matrix}

Ezzel a csiga helyzetét meghatároztuk. A kötélszárakban működő erők

\begin{matrix} P = G sin α = 67, 07 kp. \end{matrix}

A kötélszárak által bezárt szög

\begin{matrix} β = 180^{\circ} - 2 α = 83, 6^{\circ} . \end{matrix}

Horváth Sándor (Bp., I. István g. II. o. t.)
Grósz Tamás (Bp., Ságvári E. gyak. g. II. o. t.),
Takács László (Sopron, Széchenyi I. g. II. o. t.)