Kezdőlap


Feladat:	531. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Babai László , Gnädig Péter , Lábadi Albert , Pláveczky György , Steiner Gy. , Zichy L.
Füzet:	1966/január, 38 - 40. oldal		PDF \| MathML
Témakör(ök):	Csillapított rezgések, Rezgőmozgás (Tömegpont mozgásegyenlete), Munkatétel, Feladat
Hivatkozás(ok):	Feladatok: 1965/május: 531. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Vegyünk fel egy koordinátarendszert az ábrán látható módon (ebben az esetben $x_{1}$ negatív szám), és írjuk fel a mozgásegyenletet, figyelembe véve, hogy a súrlódási erő nagysága ugyan állandó, de iránya a sebesség irányától függ.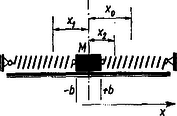

Ha a test az

x

-tengely irányításával egy irányban mozog, akkor

\begin{matrix} M a = - K_{1} x - K_{2} x - M g μ . \end{matrix}

(1)

Ha a test az

x

-tengely irányításával ellentétesen mozog, akkor

\begin{matrix} M a = - K_{1} x - K_{2} x + M g μ, \end{matrix}

(2)

ahol

M

a test tömege,

a

a gyorsulása,

K_{1}

és

K_{2}

a két rugó direkciós ereje, feladatunkban

K_{1} = K_{2} = K

. Alakítsuk át az (1) és a (2) egyenletet.

\begin{matrix} M a = - 2 K x - M g μ, ill. M a = - 2 K x + M g μ, \\ M a = - 2 K (x + \frac{M g μ}{2 K}), M a = - 2 K (x - \frac{M g μ}{2 K}) . \end{matrix}

\frac{M g μ}{2 K}

kifejezést jelöljük

b

-vel, így

\begin{matrix} M a = - 2 K (x + b), & (1a) \\ M a = - 2 K (x - b) . & (2a) \end{matrix}

Ezek az egyenletek külön-külön egy-egy súrlódás nélküli (csillapítatlan) rezgőmozgás egyenletei. Az (1a) egyenlet a

- b

, a (2a) egyenlet a

b

pont körüli rezgőmozgást írja le.
Nézzük meg a feladat szerint a test útját. A testet a kezdeti időpillanatban

x_{0}

értékkel térítettük ki. Ebben az esetben a test az

x

tengely irányításával ellentétesen mozog, tehát a (2a) egyenlet vonatkozik rá. A

b

érték körül végez olyan mozgást, mint, a csillapítatlan rezgőmozgás fél periódusa. Tehát a

b

érték a két előjeles kitérés számtani közepe.

\begin{matrix} \frac{x_{0} + x_{1}}{2} = b, x_{0} + x_{1} = 2 b, - x_{1} = x_{0} - 2 b, | x_{1} | = x_{0} - 2 b . \end{matrix}

A következő időszakban a test a másik irányba megy, tehát

\begin{matrix} \frac{x_{1} + x_{2}}{2} = - b, x_{1} + x_{2} = - 2 b, x_{2} = - x_{1} - 2 b, x_{2} = x_{0} - 4 b . \end{matrix}

Ezt tovább folytatva látszik, hogy a kitérések egy számtani sor tagjai, melynél a különbség

- 2 b

. Tehát a harmadik kitérésre:

\begin{matrix} | x_{3} | = x_{0} - 6 b . \end{matrix}

A feladat számértékeivel:

k = 50 pond/cm = 0, 5

newton/cm,

\begin{matrix} b = \frac{M g μ}{2 K} = 0, 5 cm, | x_{3} | = x_{0} - 6 b = 10 cm - 3 cm = 7 cm . \end{matrix}

Pláveczky György (Bp., I. István g. III. o. t.)

II. megoldás. Nézzük meg a feladatot a munkavégzés oldaláról. Ehhez először ki kell számítanunk a rugó potenciális energiáját. Csillapítatlan rezgőmozgás esetén a rugó teljes potenciális energiája mozgási energiává alakul. A rezgőmozgás út‐idő, sebesség‐idő és gyorsulás‐idő függvényei:

\begin{matrix} x = x_{0} sin ω t & (1) \\ v = x_{0} ω cos ω t & (2) \\ a = - x_{0} ω^{2} sin ω t = - x ω^{2} . & (3) \end{matrix}

A rezgőmozgás alapegyenlete:

m a = - K x

a = - \frac{K}{m} x

,
ezt a (3)-mal összehasonlítva látjuk, hogy

ω^{2} = \frac{K}{m}

.
Ennek a rezgőmozgásnak a

t = 0

időben nincs sebessége, tehát csak potenciális energiája van. Ez az

ω t = 90^{\circ}

-nak megfelelő időben teljes mértékben mozgási energiává alakul át, tehát az energia

\begin{matrix} E = \frac{1}{2} m v^{2} = \frac{1}{2} m x_{0}^{2} ω^{2} cos^{2} 90^{\circ} = \frac{1}{2} m x_{0}^{2} ω^{2} = \frac{1}{2} K x_{0}^{2} . \end{matrix}

x_{0}

kitéréskor a két rugó energiája

2 \cdot \frac{1}{2} K x_{0}^{2} = K x_{0}^{2}

x_{1}

kitéréskor a két rugó energiája

2 \cdot \frac{1}{2} K x_{1}^{2} = K x_{1}^{2}

,
közben súrlódás miatt végzett munka

L = M g μ (x_{0} - x_{1})

, (

x_{0}

x_{1}

x_{2}

előjeles mennyiségek). A munkavégzés egyenlete

\begin{matrix} K x_{0}^{2} - K x_{1}^{2} = M g μ (x_{0} - x_{1}), ebből \\ K (x_{0}^{2} - x_{1}^{2}) = M g μ (x_{0} - x_{1}), K (x_{0} + x_{1}) = M g μ, \\ x_{0} + x_{1} = \frac{M g μ}{K}, - x_{1} = x_{0} - \frac{M g μ}{K}, | x_{1} | = x_{0} - \frac{M g μ}{K} . \end{matrix}

A következő mozgásrésznél

\begin{matrix} K x_{1}^{2} - K x_{2}^{2} = M g μ (x_{2} - x_{1}), \end{matrix}

ebből

\begin{matrix} x_{1} + x_{2} = - \frac{M g μ}{K}, x_{2} = - x_{1} - \frac{M g μ}{K}, x_{2} = x_{0} - 2 \frac{M g μ}{K} . \end{matrix}

Láthatjuk, hogy

\begin{matrix} | x_{3} | = (x_{0} - 3 \frac{M g μ}{K} . \end{matrix}

Számértékkel:

\begin{matrix} | x_{3} | = 10 cm - 3 cm = 7 cm . \end{matrix}

Lábadi Albert (Bp., Vörösmarty g. III. o. t.)