Kezdőlap


Feladat:	506. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Almási László , Steiner György
Füzet:	1965/október, 91 - 92. oldal		PDF \| MathML
Témakör(ök):	Pontrendszer helyzeti energiája, Feladat
Hivatkozás(ok):	Feladatok: 1965/február: 506. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az egyik lehetséges elrendezés mellett (A rajz) a három henger egymás mellett fekszik a vályú alján. A középső henger $m$ tömege az $r$ rádiusz által meghatározott magasságban levő súlypontban egyesíthető, ezért a középső henger helyzeti energiája a vályú fenekéhez viszonyítva $m g r$ . A szélső hengerek középpontjának magassága $2 r$ , mert az $O_{1} O_{2} O$ háromszög mindegyik oldala $2 r$ lévén ez a háromszög szabályos háromszög, és $O_{1} K$ felezi $O_{2} O$ távolságot. Így mindegyik szélső henger helyzeti energiája $2 m g r$ , és az összes helyzeti energia 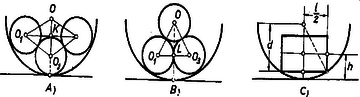$2 m g r + 2 m g r + m g r = 5 m g r$ .

Egy másik lehetséges elrendezés (B rajz), hogy két henger fekszik alul és a harmadik rajtuk. A felső henger középpontja a vályú középpontjába kerül, mert a vályú rádiusza

3 r

; ennek a hengernek

3 m g r

a helyzeti energiája.

O_{1} O_{3} O

ismét

2 r

oldalú szabályos háromszög, tehát

O L = 2 r \sqrt[]{3} / 2 = r \sqrt[]{3}

. Így

O_{1}

és

O_{3}

magassága a vályú fenekéhez képest

3 r - r \sqrt[]{3} = r (3 - \sqrt[]{3})

. A három henger összegezett helyzeti energiája

2 m g r (3 - \sqrt[]{3}) + 3 m g r = (9 - 2 \sqrt[]{3}) m g r = 5, 536 m g r

. Tehát a B rajz szerinti esetben több a helyzeti energia, és az A rajz szerinti elhelyezkedés jelenti a legkisebb helyzeti energiát. Érdekes, ha valamilyen okból mégis a B rajz szerinti helyzet alakul ki, akkor ez magától nem képes az A alatti elrendezésbe átmenni. Ugyanis a felső henger és a vályú között

2 r

szélességű csatorna van, amelyben a két alsó henger úgy mozdul el, hogy a felső henger helyén marad. A B elrendezés úgy alakulhatna át az A szerinti elrendezéssé, hogy energiabefektetéssel (aktivációs energia) felemelnénk a szélső hengereket a középső magasságáig, azután a középsőt leejtenénk és a két szélsőt hagynánk melléje gurulni.
Ugyanezen eredmények úgy is megkaphatók, ha azt keressük, hogy mikor helyezkedik el legmélyebben a három henger közös súlypontja.

Almási László (Salgótarján, Madách g. III. o. t.)

Megjegyzés. A feladat szövege nem szólt a vályú hosszáról, de triviális esettel állunk szemben, ha a vályú olyan hosszú, hogy a hengerek egymás után helyezhetők el benne. Természetesen ekkor még kisebb a helyzeti energia. A feladat szövegétől eltérően vizsgáljuk meg, mi lesz, ha a hengereket a vályú tengelyére merőlegesen helyezzük el a vályúban (C rajz). Az

l

hosszúságú henger legalul fekvő alkotója

d

mélységben van a vályú középpontja alatt. Pythagoras tételéből

{(3 r)}^{2} = {(l / 2)}^{2} + d^{2}

. Innen

d = \sqrt[]{9 r^{2} - {(\frac{l}{2})}^{2}}

. A súlypont magassága a vályú feneke felett:

h = 3 r - d + r = 4 r - \sqrt[]{9 r^{2} - {(\frac{l}{2})}^{2}}

. A három henger helyzeti energiája

3 m g h

. Ha

l = 0

, a helyzeti energia

3 m g r

, vagyis minden eddigi esetnél kisebb. Növelve a henger

l

hosszúságát a súlypont feljebb emelkedik és a helyzeti energia

l = 8 \sqrt[]{2} r / 3 = 3, 771 r

-nél éri el az

A

eset szerinti

5 m g r

értéket, majd hosszabb hengernél még nagyobb lesz. A henger lehetséges legnagyobb hossza

l = 6 r

, amikor is a helyzeti energia

12 m g r

Steiner György (Bp., Radnóti M. g. III. o.)