Kezdőlap


Feladat:	500. fizika feladat	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bodonhelyi Márta , Jakab Mihály , Takács Gábor
Füzet:	1965/szeptember, 42 - 45. oldal		PDF \| MathML
Témakör(ök):	Gördülés lejtőn, Feladat
Hivatkozás(ok):	Feladatok: 1965/január: 500. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A golyóra az $m g sin α$ mozgató erő és az ismeretlen nagyságú $S$ súrlódási erő hat. A golyó súlyának $m g cos α$ összetevőjét a lejtő kényszerereje kiegyenlíti és ezért nem vesszük számításba (1. ábra). A golyó középpontjában hozzáveszünk $+ S$ és $- S$ erőket. A golyó középpontjában $m g sin α - S$ gyorsít, és létrehoz $a$ gyorsulású mozgást, ezért a mozgástörvény alapján:

\begin{matrix} m a = m g sin α - S . \end{matrix}

(1)

1. ábra

S

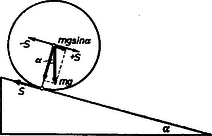súrlódási erő és a golyó középpontjában ható

- S

forgatónyomatékot jelentenek, amely az

I

tehetetlenségi nyomatékú golyót

β

szöggyorsulással forgatja (az erőkar

r

, a golyó rádiusza). A forgómozgás alaptörvénye szerint:

\begin{matrix} \frac{S r}{I} = β . \end{matrix}

(2)

Végül a golyó sima legördüléséből következik, hogy

\begin{matrix} a = β r . \end{matrix}

(3)

(Lásd A dinamikai példák megoldásáról című cikket a lap 1965. évi 2. számában.) Az (1), (2) és (3) egyenletrendszert megoldjuk

a

-ra,

S

-re és

β

-ra.

Az eredmény:

\begin{matrix} a = g \cdot \frac{m sin α}{m + \frac{I}{r^{2}}}, & (4) \\ S = m g \cdot \frac{\frac{I}{r^{2}} sin α}{m + \frac{I}{r^{2}}}, & (5) \\ β = \frac{g}{r} \cdot \frac{m sin α}{m + \frac{I}{r^{2}}} . & (6) \end{matrix}

Mindez azonban csak addig igaz, amíg a súrlódási együttható elég nagy ahhoz, hogy az (5) által kívánt súrlódási erőt létre tudja hozni. A legnagyobb súrlódási erő, amely keletkezhet:

μ m g cos α

. A súrlódási együttható kritikus értékét megkapjuk, ha ezt az (5) által megkívánt súrlódási erővel tesszük egyenlővé:

\begin{matrix} μ_{k} m g cos α = m g \cdot \frac{\frac{I}{r^{2}} sin α}{m + \frac{I}{r^{2}}} . \end{matrix}

Ennek az egyenletnek a megoldása adja a súrlódási együttható kritikus értékét:

\begin{matrix} μ_{k} = tg α \cdot \frac{\frac{I}{r^{2}}}{m + \frac{I}{r^{2}}} . \end{matrix}

(7)

Ha a súrlódási együttható ennél kisebb, akkor a golyó megcsúszik, nem gördül le simán. Ekkor az (1) és (2) alatti mozgásegyenletekbe beírjuk a súrlódási erő igénybe vett

μ m g cos α

legnagyobb értékét:

\begin{matrix} m a = m g sin α - μ m g cos α, \\ \frac{μ m g r cos α}{I} = β . & (6') \end{matrix}

Ennek az egyenletrendszernek a megoldása

β

-ra maga (6'),

a

-ra pedig:

\begin{matrix} a = g (sin α - μ cos α), \end{matrix}

(4')

a súrlódási erő pedig

μ m g cos α

.
Feladatunk számadatai mellett

α = 15^{\circ}

r = 2

cm,

m = 100

gramm,

I = 2 m r^{2} / 5 = 160 {gcm}^{2}

. Így a kritikus súrlódási együttható

μ_{k} = 0, 076

. Az első esetben,

μ = 0, 3

mellett a súrlódás elég nagy ahhoz, hogy a golyó simán gördüljön le; középpontjának gyorsulása

a = 5 g sin α / 7 = 174 {cm/sec}^{2}

, a súrlódási erő

S = 2 m g sin α / 7 = 7982

din, a szöggyorsulás

β = 5 g sin α / 7 r = 87, 1 {sec}^{- 2}

, mindez (4), (5) és (6) alapján. A második esetben,

μ = 0, 05

mellett a golyó megcsúszik; ekkor (4') és (6') alapján

a = 206 {cm/sec}^{2}

és

β = 59, 2 {sec}^{- 2}

, a súrlódási erő pedig

4735

din. A gyorsulásra kapott eredmények minden esetben függetlenek a tömegtől és a rádiusztól.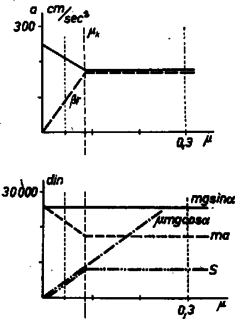

Jakab Mihály (Bp., Móricz Zs. g. III. o. t.)

2. ábra

1. megjegyzés. Vizsgáljuk meg a jelenséget állandó

α = 15^{\circ}

-os szög mellett, de a

μ

súrlódási együttható értékétől függően (2. ábra). Az ábra felső részén a golyó középpontjának gyorsulását látjuk

μ

függvényében. Súrlódás nélkül

g sin α = 244 {cm/sec}^{2}

a gyorsulás, majd

μ

növekedtével (4') szerint csökken. A kritikus súrlódási együttható elérésétől fogva

a

mindvégig

μ

-től függetlenül a (4)-ből következő

174 {cm/sec}^{2}

marad. A rajz alsó részén az erők függését tanulmányozhatjuk. A folytonos vonal a végeredményben rendelkezésünkre álló

m g sin α

erőt mutatja. Amíg a súrlódási együttható

0

és

μ_{k}

között van, az

m a

mozgató erő

a

-val arányosan csökken, az

S

súrlódási erő

μ

-vel arányosan növekszik, miközben összegük állandóan

m g sin α

marad.

μ_{k}

feletti súrlódásnál

m a

és

S

a (4)-ből és (5)-ből következő állandó értékeket veszik fel. Látható, hogy ilyenkor nem vesszük igénybe a teljes,

μ m g cos α

által megadott lehetséges súrlódási erőt. A 2. ábra felső részén a szaggatott vonal

β r

forgásból származó kerületi gyorsulást tünteti fel; látható, hogy

μ_{k}

-ig egyre csökkenő megcsúszás történik, ezután sima legördülés.

Takács Gábor (Bp., Piarista g. IV. o. t.)

2. megjegyzés. Vizsgáljuk meg a jelenséget állandó

μ = 0, 3

súrlódási együttható, de

0

-tól

90^{\circ}

-ig növekvő

α

szög mellett (3. ábra). A megcsúszás határát jelentő kritikus hajlásszöget (7)-ből számítjuk: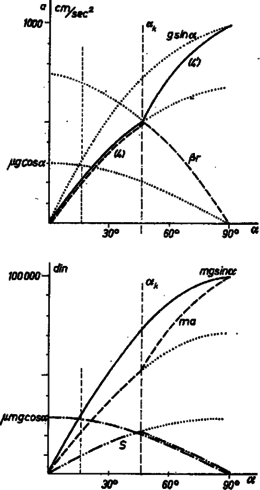

\begin{matrix} tg α_{k} = 3, 5 μ = 1, 05, α_{k} = 46^{\circ} 24' . \end{matrix}

Ennél laposabb lejtőkön sima legördülés, meredekebb lejtőkön megcsúszás következik be. A 3. ábra felső rajzán a folytonos vonal

a

gyorsulás értékét

α_{k}

-ig (4) szerint,

α_{k}

-nál meredekebb lejtőknél (4') szerint számítva tünteti fel. A 3. ábra alsó rajzán a folytonos vonal a teljes rendelkezésünkre álló

m g sin α

erőt tünteti fel. A szaggatott vonal az

a

-val arányban levő

m a

gyorsító erőt ábrázolja.

μ m g cos α

a lehetséges maximális,

S

pedig az igénybe vett súrlódási erőt mutatja. A 3. ábra felső részén a szaggatott vonal a

β r

forgásból származó kerületi gyorsulást tünteti fel; látható, hogy

0

-tól

α_{k}

-ig sima legördülés, meredekebb lejtőknél egyre növekvő megcsúszás lép fel.

3. ábra

3. megjegyzés. Megoldható a feladat a mechanikai energiamegmaradás törvényével is. A golyó helyzeti energiájának csökkenése egyenlő a végzett munkával. Abban az esetben, ha sima legördülésről van szó, a helyzeti energia csökkenése egyenlő a golyó haladó és forgó mozgásából származó energiák összegével; ekkor nem végzünk munkát a csúszó súrlódás ellen. Ha nincs sima legördülés, akkor az előbbi mozgási energia mellett a súrlódási erő ellen is végzünk munkát, amelynél az erő

μ m g cos α

, az út a csúszva és gördülve megtett utak különbsége. Ugyanazokat az eredményeket kapjuk, mint az előbbi számítással. A sima gördülés határesetében a kétféle módon számított gyorsulás egyenlő.

Bodonhelyi Márta (Bp., Móra Ferenc g. IV. o. t.)