Feladat: 366. fizika feladat Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Andor György ,  Hegedűs Csaba ,  Mészáros György ,  Simonovits András 
Füzet: 1964/február, 89 - 90. oldal  PDF  |  MathML 
Témakör(ök): Hajítások, Geometriai szerkesztések alkalmazása, Feladat
Hivatkozás(ok):Feladatok: 1963/május: 366. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Az 1960. évi tanulmányi verseny II. fordulójának 3. példája alapján a lejtőre történő becsapódási szög tangensét az 1tgα-2tgβ kifejezés adja, ahol α a kilövés, β a lejtő hajlásszöge. Ez a szög jelen esetben 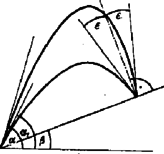β±ε.
Tehát:

tg(β±ε)=1tgα-2tgβ.
A két oldal reciprokát véve:
ctg(β±ε)=tgα-2tgβ.
Rendezve: tgα=2tgβ+ctg(β±ε).
 
 
1. ábra
 

Minden szóba jöhető esetben (0∘≤β<90∘ és 0∘≤ε<90∘), a β=ε esetet kivéve mindig két megoldás van, ugyanis a kilövés nemcsak a lejtőn felfelé, hanem lefelé is történhet, amit a tgα-ra kapott negatív eredmény, vagy tgα<tgβ eset jelez. Ha β=ε, akkor ctg(β-ε)=ctg0∘ értelmetlen volta miatt csak egy megoldás van.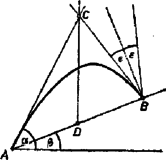
 
 Andor György (Bp., Rákóczi F. g. III o. t.)
 
II. megoldás. A kilövés szögét szerkesztéssel is meghatározhatjuk, ugyanis a lövedék parabola pályájának ismert két pontja: az A kilövési pont és a B becsapódási pont (B-t tetszés szerint felvehetjük a lejtőn, mert ettől csak a kilövés sebessége függ), másrészt ismert még a B pontbeli érintő, mert a becsapódás pillanatában a sebesség a lejtőre emelt merőlegessel adott ε szöget zár be. Végül még azt is tudjuk, hogy a parabola tengelyének iránya függőleges.
 
 
2. ábra
 

A kilövési szög meghatározása egyértelmű az A pontbeli érintő megszerkesztésével. Ehhez pedig a következő ismert tételt használhatjuk fel. A parabola két érintőjének metszéspontja és az érintési pontokat összekötő szakasz felezőpontja által meghatározott egyenes párhuzamos a parabola tengelyével.
Ezek alapján a szerkesztés menete: meghúzzuk a B ponton átmenő érintőt, és meghatározzuk az AB szakasz felezőpontján, D-n átmenő függőleges egyenessel alkotott metszéspontját, C-t. Ha C a lejtő felett van, akkor az AC iránya megadja a kilövés szögét. Hogy az összes megoldást megkapjuk, célszerű egy‐egy B pontot az A alatt, illetve felett felvenni.
 
 Hegedűs Csaba (Nagykanizsa, Landler J. g. III. o. t.)