Kezdőlap


Feladat:	355. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Makai Endre , Máthé István , Mezei Ferenc
Füzet:	1964/január, 40 - 41. oldal		PDF \| MathML
Témakör(ök):	Munkatétel, Síkinga, Közelítő számítások, numerikus módszerek, Feladat
Hivatkozás(ok):	Feladatok: 1963/március: 355. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az impulzusmomentum megmaradása az inga esetében nem érvényes, mert a rendszer nem zárt: a testre ható nehézségi erő forgatónyomatéka (a forgáspontra vonatkoztatva) nem állandóan zérus. Ez nyilvánvaló is, hiszen a szélső helyzetekben az impulzusmomentum zérus, középen maximális nagyságú. Így, bár a fonalhosszat változtatható erő forgatónyomatéka zérus (a tengelyben hat), az amplitudónövelést az impulzusmomentum megmaradásának tétele nem tiltja, hiszen e tételnek az ingához mint nem zárt rendszerhez semmi köze. Így a megoldás során nem is alkalmazható. Feltesszük, hogy a hosszváltoztatást ,,lassan'' hajtjuk végre. Ezen azt értjük, hogy nincs rugalmatlan ütközést jelentő rántás vagy a fonál hirtelen meglazulása, továbbá a fellépő hosszváltoztató gyorsulások oly kicsik, hogy a fonálban ható erőt lényegesen nem befolyásolják. (Ez azt jelenti, hogy $g$ -hez viszonyítva kis gyorsulásokkal dolgozunk.)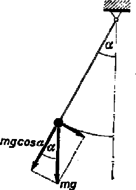
Az energiamegmaradás elvét alkalmazzuk. Amikor a fonalra a legnagyobb erő hat (középen), felhúzzuk egy kicsit a fonalat, majd a legkisebb feszítő erő mellett (szélen) visszaengedjük. Így energiát közlünk a lengő rendszerrel. Amikor középen kicsiny $Δ l$ hosszal a testet felhúzzuk, akkor $m g$ $Δ l$ helyzeti energiát nyert a rendszer. A szélen a fonalat csak $m g cos α$ erő feszíti (l. az ábrát) tehát ha itt lassan visszaengedjük, akkor a lengőrendszer rajtunk $m g cos α \cdot Δ l$ munkát végez, azaz ennyi energiát veszít. De most az ingahossz már az eredeti, így a lengésamplitudó növekedésével raktározhatja csak az inga a felvett $Δ E = m g Δ ℓ - m g cos α \cdot Δ ℓ = m g Δ ℓ (1 - cos α)$ energiát.

Ismeretes, hogy ha a maximális szögkitérés

α

(radiánban), akkor a lengő test amplitudója

A = ℓ α

(

ℓ

az ingahossz,

α

kicsi), így a maximális sebesség

v = A ω = ℓ α ω

(

ω

a körfrekvencia:

ω = \sqrt[]{g / ℓ}

) tehát az inga energiája:

\begin{matrix} E = m v^{2} / 2 = m {(ℓ α ω)}^{2} / 2 = m g ℓ α^{2} / 2. \end{matrix}

(1)

(Ugyanis amikor középen

v

maximális, akkor a helyzeti energia 0-nak vehető, a szélső helyzetben pedig csak helyzeti energia van. A kettő összege állandó a lengés során.) (1)-ből a maximális szögkitérés négyzete:

α^{2} = 2 E / m g ℓ

, míg a megnövekedett

α'

négyzete:

α'^{2} = \frac{2 (E + Δ E}{m g ℓ}

.

Ezzel lényegében a feladatot megoldottuk. A következőkben néhány matematikai közelítés útján áttekinthetőbbé tesszük eredményünket.
Legyen

α' = α + Δ α

. Ekkor:

\begin{matrix} \frac{2 (E + Δ E)}{m g ℓ} - \frac{2 E}{m g ℓ} = \frac{2 Δ E}{m g ℓ} & = α'^{2} - α^{2} = α^{2} + 2 α \cdot Δ α + {(Δ α)}^{2} - α^{2} = \\ = 2 Δ α \cdot α + {(Δ α)}^{2} . \end{matrix}

Mivel

Δ α

sokkal kisebb, mint

α

(hiszen

Δ ℓ

, ill.

Δ E

is kicsi

ℓ

-hez ill.

E

-hez képest), ezért az utolsó tag sokkal kisebb az előtte állónál, így elhanyagolható. Marad tehát

\begin{matrix} \frac{2 Δ E}{m g ℓ} = 2 α \cdot Δ α . \end{matrix}

Így az amplitudónövekedés:

\begin{matrix} Δ α = \frac{Δ E}{α m g ℓ} = \frac{m g Δ ℓ (1 - cos α)}{α \cdot m g ℓ} = \frac{Δ ℓ}{ℓ} \cdot \frac{1 - cos α}{α} = \frac{Δ ℓ}{ℓ} \cdot \frac{2 sin^{2} \frac{α}{2}}{α} . \end{matrix}

Mivel

α

kis szög,

sin \frac{α}{2} \approx \frac{α}{2}

(

α

-t radiánban mértük!), így végül:

\begin{matrix} Δ α = \frac{Δ ℓ}{ℓ} \cdot \frac{2 {(α / 2)}^{2}}{α} = \frac{Δ ℓ}{ℓ} \cdot \frac{α}{2}, ill. \frac{Δ A}{A} \approx \frac{Δ α}{α} = \frac{1}{2} \frac{Δ ℓ}{ℓ}, \end{matrix}

azaz a relatív amplitudónövekedés a relatív hosszváltoztatásnak közelítőleg a fele.

Mezei Ferenc