Kezdőlap


Feladat:	350. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Pelikán József , Török Katalin
Füzet:	1964/január, 35 - 37. oldal		PDF \| MathML
Témakör(ök):	Erők forgatónyomatéka, Tapadó súrlódás, Feladat, Merev test egyensúlya
Hivatkozás(ok):	Feladatok: 1963/március: 350. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük $α$ -val $P$ -nek a függőleges lappal bezárt szögét, és tegyük fel, hogy $P$ eleget tesz a feladat követelményeinek. Először azt vizsgáljuk, hogy $α$ függvényében melyik él mentén történik az elfordulás.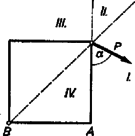
Ha $0^{\circ} < α \leq 135^{\circ}$ , akkor $A$ és $B$ élre nézve a forgatónyomatékok iránya azonos, ezért csak egy irányban, az óramutató járásával egyező irányban lehetséges az elfordulás. Ez azt jelenti, hogy ekkor a felborulás csak az $A$ él mentén lehetséges.

Hasonlóképpen, ha

180^{\circ} \leq α < 315^{\circ}

, akkor a felborulás csak a

B

él mentén történhet.

315^{\circ} \leq α \leq 360^{\circ}

esetén egyáltalán nem lehetséges a felborulás, mert a kockára ható erők eredője okvetlenül átmegy az alátámasztási felületen.
Utoljára maradt a legbonyolultabb eset:

135^{\circ} < α < 180^{\circ}

; ekkor ugyanis

A

élre negatív,

B

-re pedig pozitív forgatónyomaték hat. Nagyban egyszerűsödik a probléma, ha megengedünk egy bizonyos kezdeti lökést, amelynek hatására mindig csak az egyik él marad az alappal érintkezésben, de ez oly kicsi elmozdulást hoz létre, hogy az erőkkel úgy számolhatunk, mintha nem lenne elmozdulás. Mivel ekkor a forgástengelyül szolgáló élt ez a kezdeti lökés határozza meg, ezért itt mindkét irányú elfordulást lehetségesnek vehetjük.
Tehát az

A

él körül

0^{\circ} < α < 180^{\circ}

esetén, a

B

él körül

135^{\circ} < α < 315^{\circ}

esetén történhet a felborulás.
Ezután pedig határozzuk meg az

A

él körüli felborulás többi feltételét is. Bontsuk fel

P

-t vízszintes és függőleges irányú összetevőkre.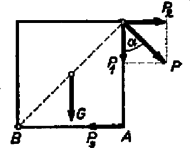

Nincs elcsúszás, ha a súrlódási erő nagyobb, mint

P_{2}

\begin{matrix} P sin α \leq P_{s} . \end{matrix}

Másrészt

P_{s}

-ről tudjuk, hogy 0 és

P_{n} μ = (G + P_{1}) μ = (G + P cos α) μ

közötti értékeket vesz fel. Ebből

\begin{matrix} P sin α \leq (G + P cos α) μ, \end{matrix}

rendezve:

\begin{matrix} 1 / μ \cdot P sin α - P cos α \leq G adódik . \end{matrix}

(1)

Másik szükséges feltétel, hogy a

P

forgatónyomatéka az

A

élre nagyobb legyen, mint a súlyerőé:

\begin{matrix} (a / 2) G \leq a P sin α, \end{matrix}

egyszerűsítve:

\begin{matrix} G \leq 2 P sin α . \end{matrix}

(2)

(1) és (2) összevetésével.

P (1 / μ \cdot sin α - cos α) \leq G \leq 2 P sin α

, látható, hogy ez a feltétel egyben elegendő is.

Így

(1 / μ - 2) sin α = cos α

, azaz

ctg α \geq 1 / μ - 2

szükségessége következik. Tehát adott

μ

esetén

α

-nak bármely szöget választhatunk a

0^{\circ}

-tól az

α_{max} = arc ctg (1 / μ - 2)

-ig terjedő intervallumban. (Ha

μ = 1 / 2

α_{max} = 90^{\circ}

;

μ = 1

esetén

α_{max} = 135^{\circ}

P

választása pedig:
Ha

tg α > μ

, akkor (1) és (2)-ből (a nevezők pozitívak):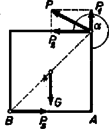

\begin{matrix} \frac{G}{2 sin α} \leq P \leq \frac{G}{1 / μ sin α - cos α}, ha pedig \end{matrix}

tg α \leq μ

, akkor a feltétel:

\frac{G}{2 sin α} \leq P

, (2) viszont eleve teljesül, ugyanis ilyenkor a nevező negatív. Ezért ilyen esetben

P

-nek csak minimuma van; maximuma nincs.

Végül vizsgáljuk a

B

él körüli felborulás feltételeit (

135^{\circ} < α < 315^{\circ}

).
Az el nem csúszás feltétele az előzőhöz hasonlóan:

\begin{matrix} P | sin α | \leq (G + P cos α) μ \end{matrix}

(abszolút érték azért kell, mert a

sin α 180^{\circ}

-nál előjelet vált), ebből

\begin{matrix} P (1 / μ \cdot | sin α | - cos α) \leq G . \end{matrix}

Másrészt a felborulás feltétele:

P_{1} a + P_{2} a \geq \frac{G}{2} a

, ahol

P_{1} = - P cos α

és

P_{2} = - P sin α

, mivel a forgatás az előzővel ellentétes; ebből

\begin{matrix} - 2 P (cos α + sin α) \geq G . \end{matrix}

(4)

(3)-t és (4)-t összevetve:

\begin{matrix} P (1 / μ \cdot | sin α | - cos α) \leq - 2 P (cos α + sin α) . \end{matrix}

Nézzük először azt az esetet, amikor

135^{\circ} < α < 180^{\circ}

; ekkor

| sin α | = sin α

.

Behelyettesítve és rendezve:

(1 / μ + 2) sin α \leq - cos α

.
Tehát:

ctg α \leq (1 / μ + 2)

180^{\circ} \leq α < 315^{\circ}

esetén

| sin α | = - sin α

. Ezt behelyettesítve kapjuk:

\begin{matrix} ctg α \geq (1 / μ - 2) . \end{matrix}

Az előzőhöz hasonló feltételeket kapunk

P

-re is:
Ha

1 / μ \cdot | sin α | - cos α > 0

, akkor

\frac{G}{- 2 (cos α + sin α)} \leq P \leq \frac{G}{1 / μ \cdot | sin α | - cos α}

-nak kell teljesülnie, ha pedig ez nem teljesül, akkor

P

-nek nincs felső határa.

Török Katalin (Bp., Patrona Hungariae lg. II. o.t.)