Kezdőlap


Feladat:	334. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Batta Gyula , Doskar Balázs , Kiss G.
Füzet:	1963/december, 227 - 228. oldal		PDF \| MathML
Témakör(ök):	Összetartó erők eredője, Feladat, Merev test egyensúlya
Hivatkozás(ok):	Feladatok: 1963/február: 334. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Először számítsuk ki a szükséges geometriai adatokat. A három nagy golyó középpontjai $2 R$ oldalú szabályos háromszöget alkotnak, amelynek magassága $O_{1} T = R \sqrt[]{3}$ . Az $O$ felfüggesztési pontból e háromszög síkjára merőlegesen rajzolt függőleges egyenes a $2 R$ oldalhosszúságú szabályos háromszöget $C$ középpontjában találja el: $O_{1} C = 2 \sqrt[]{3} R / 3$ . A kis golyó középpontja $K$ -ban van: $O_{1} K = R + r$ . Továbbá $α = C K O_{1} ∢ = 40^{\circ} 30'$ , mert $sin α = O_{1} C / O_{1} K = 0, 648$ . A kis golyónak a fonállal alkotott alsó érintkezési pontját, $A$ -t az $O_{1} A = 5 + 3 = 8$ cm-es körívvel való kimetszés adja meg. $A K O_{1} ∢ = ϑ = 64^{\circ}$ , mivel $cos ϑ = \frac{r}{r + R} = 0, 439$ . Az $A B$ ív hossza 2 cm, $A K B ∢ = φ = 30^{\circ}$ . Végül a $B K$ -ra rajzolt merőleges adja meg $O$ -t, a felfüggesztési pontot: $B O = 4$ cm. A fonál felső részének a függőlegessel alkotott szöge 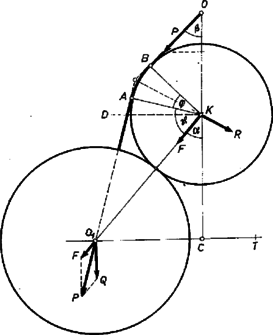$B O K ∢ = β = B K D ∢ = α + ϑ + φ - 90^{\circ} = 44^{\circ} 30'$ .

1. ábra

O_{1}

-ben hat a nagy golyó

G

súlya. Ez a nagy golyó attól az állapottól kezdve mozdul meg, amikor a kis golyó részéről az

O_{1} K

irányban ható

F

erő és

G

súlyerő eredője a fonál

O_{1} A

irányába esik. Ezt az

F

erőt nemcsak a kis golyó

q

súlya, hanem a ráfeszülő fonáltól eredő

R

erő is okozza. Az

O_{1} A

irányában ható

P

fonálerőt szinusz tétellel számítjuk ki:

\begin{matrix} P : Q = sin α : cos ϑ, \end{matrix}

ugyanis

Q P O_{1} ∢ = A O_{1} K ∢ = 90^{\circ} - ϑ

. Tehát a fonálban ható erő a megmozdulás határesetében:

\begin{matrix} P = Q \frac{sin α}{cos ϑ} = 1, 476 Q = 7, 38 kp. \end{matrix}

Tekintettel arra, hogy nincs súrlódás, pontosan ez az erő hat a fonál legfelső részében

B O

irányban. Ennek az erőnek a függőleges összetevője:

\begin{matrix} P cos β = Q \frac{sin α cos β}{cos ϑ} \end{matrix}

Ennek az erőnek a háromszorosa tartja az

O

-pontban a

3 Q + q

súlyt, ezért

\begin{matrix} 3 Q \frac{sin α cos β}{cos ϑ} = 3 Q + q . \end{matrix}

Innen a kis golyó megengedhető legnagyobb súlya:

\begin{matrix} q = 3 Q [\frac{sin α cos β}{cos ϑ} - 1] = 0, 156 Q = 0, 78 kp . \end{matrix}

Tehát a kis golyó ezen súlyánál kezdenek a nagy golyók szétválni egymástól. De mégsem ez a felelet a kérdésre. A feladat a kis golyó átesésének feltételét kérdezte. Az ábrából látható, hogy a nagy golyó kis szétnyílásánál

α

nagyobb,

β

kisebb lesz, és

ϑ

állandó marad, így a kis golyó lesüllyedése közben mindig nagyobb és a nagyobb erő szükséges az egyensúly‐állapot fenntartásához. Mindez addig tart (második ábránk), amíg a fonál a kis gömb érintője nem lesz

H

-ban. Ekkor

φ = 0

, és

α + ϑ = 90^{\circ} + β

, ezért

ϑ = 90^{\circ} - (α - β)

. Tehát a kis golyó azon súlya, amely mellett a fonál a kis golyó érintőjévé lesz: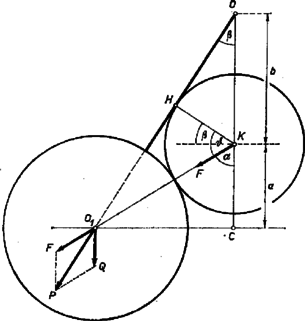

\begin{matrix} q = 3 Q \frac{sin α cos β}{sin (α - β)} - 1 = 3 Q \frac{sin α cos β - sin (α - β)}{sin (α - β)} = \\ = 3 Q \frac{cos α sin β}{sin α cos β - cos α sin β} = 3 Q \frac{cotg α}{cotg β - cotg α} = \\ = 3 Q \frac{O_{1} C cotg α}{O_{1} C cotg β - O_{1} C cotg α} = 3 Q \frac{a}{a + b - a} = 3 Q \cdot \frac{a}{b} \end{matrix}

2. ábra

Ez az egyensúlyfeltétel azonos a hozzá nem érő kötél számára levezetett, az 1962. évi Eötvös versenyből ismert megoldással. Ekkor

α = 58^{\circ} 52'

β = 32^{\circ} 52'

a = 4, 6

cm,

b = 7, 1

cm és

q = 3 Q \cdot 0, 648 = 1, 944 Q = 9, 72

kp. A versenyfeladatból ismeretes, hogy azután tovább növelve a terhelést, a golyó átesik.
Összefoglalva az eredményt, 0-tól

0, 78

kp-ig semmi sem történik,

0, 78

-tól

9, 72

kp-ig a golyók mindig jobban szétállnak, végül

9, 72

kp felett a kis golyó átesik.

Doskar Balázs (Bp., Piarista g. III. o. t.) dolgozata alapján