| Feladat: | 306. fizika feladat | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Megoldó(k): | Corradi Gábor , Doskar Balázs , Hirka András , Mészáros Gy. | ||
| Füzet: | 1963/október, 89 - 90. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Súlypont (tömegközéppont) meghatározása, Összetartó erők eredője, Feladat, Merev test egyensúlya | ||
| Hivatkozás(ok): | Feladatok: 1962/december: 306. fizika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A függő golyók helyzetét az a szög határozza meg, amelyet a érintkezési pontból az felfüggesztési pontba húzott egyenes zár be a függőlegessel. jelzi a két golyó közös súlypontját, amely az felfüggesztési pont alatt helyezkedik el. az távolságot a súlyokkal fordított arányban osztja két részre, ezért 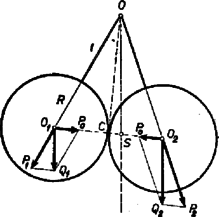 A súlypont távolsága a felfüggesztési ponttól: Az erők meghatározása céljából és golyósúlyokat felbontjuk a tartófonal irányába eső és az érintkezési pont felé mutató összetevőkre ( és , valamint és nagyságúak). Hasonló háromszögekből: A fonalakat feszítő erőket ugyanezekből a hasonló háromszögekből kapjuk: Hirka András (Pannonhalma, Bencés g. III. o. t.) |