Kezdőlap


Feladat:	300. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bodonhelyi Márta , Dobozy Ottó , Nagy Klára , Ordódy Márton , Patkós András , Szabó M. , Szentai Judit , Zichy László
Füzet:	1963/szeptember, 41 - 43. oldal		PDF \| MathML
Témakör(ök):	Szabadesés, Tökéletesen rugalmatlan ütközések, Tökéletesen rugalmas ütközések, Tömegközéppont mozgása, Feladat
Hivatkozás(ok):	Feladatok: 1962/december: 300. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Fel fogjuk használni azt a tényt, hogy három egyenlő tömegű tömegpont egy egyenes mentén való mozgása esetén közös súlypontjuk sebessége és gyorsulása az egyes tömegpontok megfelelő előjellel ellátott sebességeinek ill. gyorsulásainak számtani közepe (1. a megjegyzést).

Vegyük észre, hogy az esés ideje éppen

1 sec . (g t^{2} / 2 = 4, 9 m, innen t^{2} = 2 \cdot 4, 9 m / g = 1 {sec}^{2} .)

Grafikusan az első golyó útját az idő függvényében parabola ábrázolja:

s = g t^{2} / 2

. A súlypont gyorsulása csak (

g + 0 + 0) / 3 = g / 3

, a magasságot tehát egy

1 : 3

arányban lapított parabola ábrázolja. Végpontja

4,9 \cdot 2 / 3 = 3, 27 m

magasan lesz. Ezután csak a második golyó végez szabadesést, azért ismét

g / 3

lesz a súlypont gyorsulása, így az előbbi út‐idő grafikon valósul meg, a

h = 3, 27 m

pontból indulva

4, 9 / 3 = 1, 63 m

-ig. Majd ez ismétlődik még egyszer. (Kezdősebesség egyik szakasz elején sincs!)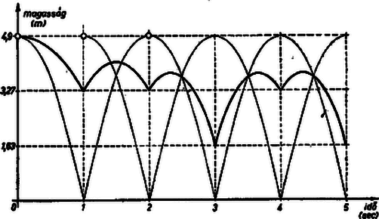

Rugalmas ütközés esetén az első sec alatt ugyanaz történik, mint előbb. Ezután az első golyó

v_{0} = g \cdot 1 sec

sebességgel visszapattan, és a második is esni kezd. A két golyó gyorsulása egyaránt

g

(lefelé). A súlypont felfelé irányuló

(v_{0} + 0 + 0) / 3 = v_{0} / 3

kezdősebességgel rendelkezik, gyorsulása lefelé

(g + g + 0) / 3 = 2 g / 3

lesz. Ez tehát lényegében egy függőleges hajítás, az emelkedés idejére (1. pl. a 299. feladat megoldását)

v_{0} / 3 = 2 g \cdot t_{0} / 3

teljesül, így

t_{0} = 0, 5 sec

, az emelkedési magasság:

(2 g / 3) \cdot t^{2} / 2 = g / 12 m = 0, 85

méter. Ezért a

2 sec

végén a súlypont visszaérkezik a

3, 27 m

magasságba, míg közben a

t = 1, 5 sec

időpontban

3, 27 + 0, 85 = 4, 12

m magasságig emelkedett. Ezután a második golyó ismét

v_{0}

sebességgel visszapattan, az első és a harmadik együtt indul kezdősebesség nélkül fentről. Most mindhárom golyó esik, tehát lefelé gyorsul. Így a tömegközéppont kezdősebessége ismét

(0 + v_{0} + 0) = v_{0} / 3

és felfelé irányul, gyorsulása

(g + g + g) / 3 = g

lefelé: ismét függőleges hajítás. Az emelkedés ideje most

\frac{v_{0} / 3}{g} = \frac{g \cdot 1 sec/3}{g} = 1 / 3 sec

, a magasság

g / 2 {(\frac{1}{3})}^{2} = 0, 58 m

, tehát a súlypont

3, 27 + 0, 54 = 3, 81 m

magasságig emelkedik, majd innen

2 / 3 sec

-ig, azaz

g / 2 \cdot {(2 / 3)}^{2} = 2, 18

métert szabadon esik, tehát a

3. sec

végén

3, 81 - 2, 18 = 1, 63 m

magasan lesz, ami természetesen megfelel a golyók helyzetének. A következő sec-ban a golyók mozgása ellentétes irányban ugyanaz lesz, mint most volt, így a súlypont is ugyanilyen módon visszajut a

3, 27 m

-es kiindulási helyzetbe; majd az előbbi ismétlődik.

Dobozy Ottó (Bp., Apáczai Cs. J. gyak. isk. VII. o. t.)
dolgozata alapján

Megjegyzés: Bebizonyítjuk a kiindulásul felhasznált tényt. Vegyünk fel egy egyenest 0 kezdőponttal, és jelöljük ki rajta a pozitív irányt (3. ábra). Helyezkedjenek el az egyenlő tömegű tömegpontok ezen az egyenesen 0-tól

x_{1}

x_{2}

, ill.

x_{3}

előjeles távolságra. Ekkor a súlypontjukat pl. így határozhatjuk meg: az 1. és 2. tömegpont súlypontja a köztük levő szakasz

S

felezőpontja, tehát

(x_{1} + x_{2}) / 2

. Ezután ebben a pontban gondoljuk egyesítve az 1. és 2. testeket, ekkor ezek és a 3. test súlypontja az őket összekötő szakasz

S

-hez közelebbi harmadolópontja, hiszen

S

-ben kétszeres tömeg ,,van''. Ezt a pontot pl. úgy kapjuk meg, hogy

S

-től felmérjük az

S

-től a 3. pontig terjedő szakasz 1/3 részét:

\begin{matrix} \frac{x_{1} + x_{2}}{2} + \frac{1}{3} (x_{3} - \frac{x_{1} + x_{2}}{2}) = \frac{x_{3}}{3} + \frac{2}{3} \frac{x_{1} + x_{2}}{2} = \frac{x_{1} + x_{2} + x_{3}}{3} . \end{matrix}

Mozduljon el egy

Δ t

idő alatt a három tömegpont előjel szerint

Δ x_{1}

Δ x_{2}

, ill.

Δ x_{3}

szakasszal. Ekkor a súlypont elmozdulása

\begin{matrix} x = \frac{(x_{1} + Δ x_{1}) + (x_{2} + Δ x_{2}) + (x_{3} + Δ x_{3})}{3} - \frac{x_{1} + x_{2} + x_{3}}{3} = (Δ x_{1} + Δ x_{2} + Δ x_{3}) / 3. \end{matrix}

Így a súlypont átlagsebessége

\begin{matrix} \frac{Δ x}{Δ t} = (\frac{Δ x_{1}}{Δ t} + \frac{Δ x_{2}}{Δ t} + \frac{Δ x_{3}}{Δ t}) / 3. \end{matrix}

Mivel ez akármilyen kis

Δ t

-re igaz, ezért hasonló összefüggés áll fenn a pillanatnyi sebességek közt is. Ugyanígy látható be az állítás a gyorsulásra, ill. általában akárhány tömegpontra.