Feladat: 247. fizika feladat Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Góth László ,  Nagy Dénes Lajos ,  Rácz Mátyás ,  Schaub Zsuzsanna 
Füzet: 1962/november, 181 - 182. oldal  PDF  |  MathML 
Témakör(ök): Egyéb felületi feszültség, Függvények grafikus elemzése, Feladat
Hivatkozás(ok):Feladatok: 1962/április: 247. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a szabályos n-szög r sugarú körbe írva és oldala an=2rsinπ/n=qr. Egy függőleges és egy ferde síkú háromszög területének összege: F=r/2(M-x)+an/2m2+x2=rM/2-rx/2+qr/2⋅r2-q2r2/4+x2. Ezen mennyiség n-szeresének minimumhelyét kell vizsgálnunk. Ahelyett nyilván kereshetjük F, illetve ‐ rM/2 állandó lévén ‐ qr/2r2-q2r2/4+x2-xr/2 minimumát, vagy ezt r/2-vel osztva, b2=r2(1-q2/4) jelöléssel az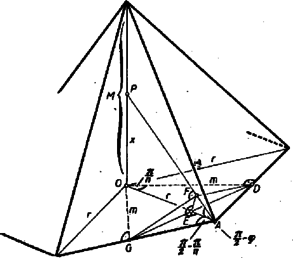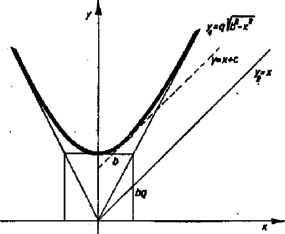
y=qb2+x2-x függvény minimumhelyét.

 
 
1. ábra
 
 
2. ábra
 

Az y1=qb2+x2 függvény az y12/q2=b2+x2, vagyis az y12/b2q2-x2/b2=1 hiperbola felső ágának egyenlete, ezen hiperbola valós tengelye az y-tengely. Az y1 függvény és az y2=x függvény különbségének minimumát keressük, ez a rajz szerint nyilván azon x érték mellett következik be, amelyben az y2=x egyenessel párhuzamos 45∘-os egyenes érinti a felső hiperbolaágat. Ilyen egyenes csak q>1 esetén létezik az ábra szerint. Tehát a 2sinπ/n≦1, vagyis az n≧6 esetekben az y függvény a 0≦x≦M intervallum valamelyik végénél, a 2 intervallumvégben felvett értéket összehasonlítva könnyen látható, hogy x=M mellett veszi fel a legkisebb értéket. Ez azt jelenti, hogy ha a szappanhártya a feltételezett módon alakul ki, akkor ezen esetekben a palástot kell befednie.
Annak feltétele, hogy az y=x+c egyenes érintse a hiperbolaágat, az, hogy a
c+x=qb2+x2, tehát a(c+x)2=q2(b2+x2)-ből adódó(q2-1)x2-2cx+q2b2-c2=0


másodfokú egyenlet diszkriminánsa 0 legyen (egyetlen közös pont):
4c2-4(q2-1)(q2b2-c2)=0, amibőlc=bq2-1.


Így az érintési pont koordinátája (x=-b2a a másodfokú egyenlet együtthatóinak szokásos jelölésével):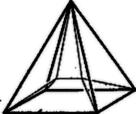
x=2bq2-12(q2-1)=r24-q2q2-1=rcosπ/n4sin2π/n-1(n=3,4,5)
behelyettesítések, egyszerűsítés után. Ebből x az n=4, 5 speciális esetekre is könnyen kiszámítható.
 
 
3. ábra
 

Most nézzük meg, mekkora x mellett lehetnek 120∘-os lapszögek. Ha n≧4, 120∘-os lapszögekről a függőleges síkok esetében nyilvánvalóan nem beszélhetünk. Egy ferde élhez csatlakozó lapoknál pedig a szimmetriát figyelembe véve elegendő, ha a két ferde sík szöge 120∘. Képzeljük úgy, hogy két szomszédos alapél felezéspontján át (D, G) az AP élre merőleges síkot fektetünk, ez OA-t E-ben, AP-t F-ben metszi, az alappal φ szöget alkot. EA∢=π(2-π)n, melynek egyik szára DE-vel derékszöget alkot, az előbb mondott síkon vett merőleges vetülete EFD∢=π/3 kell, hogy legyen; itt EF⊥DE a szimmetriaviszonyok miatt. Ezért DE-t egységnek tekintve AE=ctg(π(2-π)n)=tg π/n, EF=ctg π/3=3, tehát az AEF△
-ből cosφ=sin(π/2-φ)=EF=3/tgπ/n. Azonban
cosφ=11+tg2φ=11+r2/x2,s így11+r2/x2=3tgπ/n, ahonnanx=r3tg2π/n-1,


s ez nyilván azonos az előbb kapott eredménnyel; csak n=3, 4, 5-re van értelme.
Ha n≧6, akkor már azért sem lehetnek 120∘-os lapszögek, mert akkor DAE∢≧60∘, s így a DAE és FAE lapok szöge, DFE∢≧60∘, mivel a lapszög az ilyen szögek közötti maximális szöggel egyenlő.
 
 Schaub Zsuzsanna (Győr, Kazinczy lg. IV. o. t.) és
 Nagy Dénes Lajos (Bp., Rákóczi g. IV. o. t.) dolgozata alapján.
 

Megjegyzés: A valóságban már n=4 esetében is másként helyezkedik el a hártya, görbült élekkel: (3. ábra). Ugyanis 3-nál több hártya összefutása egy élben labilis.
 
 Nagy Dénes Lajos (Bp., Rákóczi g. IV. o. t.)