Feladat: 244. fizika feladat Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Bodrogi Árpád ,  Holler Zsuzsanna 
Füzet: 1962/november, 178 - 179. oldal  PDF  |  MathML 
Témakör(ök): Egyéb mozgás lejtőn, Merev test egyensúlya, Feladat
Hivatkozás(ok):Feladatok: 1962/április: 244. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A kétágú lejtőre szimmetrikusan elhelyezett kettőskúp úgy van nyugalomban, ha bármely szimmetrikus elmozdulása közben tengelye vízszintes síkban mozog. (Nyilvánvalóan a szimmetrikus kényszerviszonyok csak szimmetrikus helyzetű elmozdulást engedélyeznek.)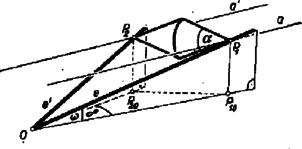
Tételezzük fel, hogy sikerült a lejtőt a kívánt módon szétnyitni. Ha most a kúpot végiggörgetjük a két egyenesen, akkor ennek A ill. A' csúcspontja a vízszintes helyzetű, egymással párhuzamos a ill. a' egyeneseket írja le. A kettőskúp minden helyzetében e ill. e' egyenes érinti a kúppalástot. Ha az érintkezési pontokban megrajzoljuk a kúppalástot érintő S ill. S' síkokat, kiderül a következő:
e ill. e' egyenes benne fekszik az S ill. S' síkban;
az a ill. a' egyenesen elhelyezkedő kúpcsúcs szintén illeszkedik S-re ill. S'-re;
az e egyenes, valamint az a egyenes valamely pontja által meghatározott sík a csúcspont helyzetétől függetlenül mindig ugyanaz, nevezetesen amelyet a metsző a és e egyenesek határoznak meg.

 
 

Ebből mindjárt következik, hogy a kettőskúp minden szimmetrikus helyzetében az a és e egyenesek, illetve a' és e' egyenesek által kifeszített sík S ill. S'-vel azonos.
Amikor a kettőskúp a lejtők közös O pontjához jut, alapköre érinti az S és S' síkok vízszintes metszésvonalát. (S és S' metszésvonala azért vízszintes, mivel a∥a' vízszintes egyenesek.)
A mondottakból kiderül, hogy a kúp fenti szélső helyzetében a középpont függőlegesen O fölött R távolságban van.
A kúp másik végállapotában a két csúcspont a és e, valamint a' és e' P1 ill. P2 metszéspontjában van. Itt a kúp középpontja az alapsíktól P1P10 távolságnyira van.
A feladat épp az, hogy δ megválasztásával biztosítsuk a P1P10=R esetet. A gondolatmenetből ugyanis kitűnik, hogy épp a fenti egyenlőség szükséges és elegendő az egyensúlyi helyzethez.
 

P1P10=P10P20=2Rtg α2, a feltétel folytán OP10=Rtg ω, így végül sinδ02=tg ωtg α2.
 

A feladatban szereplő értékekkel δ0=111,12 adódik.
Belátható könnyen, hogy
δ>δ0esetén a kúpO-tól távolodva,δ>δ0esetén pedigO felé gördül.