Kezdőlap


Feladat:	467. fizika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Ábrahám Csongor , Almási Kristóf , Bacsó Zsolt , Danyi Pál , Guba Kornél , Puppán István , Seregdy Tamás , Temesi László
Füzet:	1980/január, 33 - 35. oldal		PDF \| MathML
Témakör(ök):	Egyenletes mozgás (Egyenes vonalú mozgások), Hangsebesség, Gyakorlat
Hivatkozás(ok):	Feladatok: 1979/május: 467. fizika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A pályához egy számegyenest illesztünk olyan módon, hogy a sípoló vonat a jeladás első pillanatában (innen számítjuk az időt) a skála nullpontjában legyen, és a pozitív féltengely felé haladjon $v_{1}$ sebességgel. Két alapvető esetet különböztetünk meg.
Az első esetben $t = 0$ -ban az ismeretlen sebességű vonat a pozitív féltengely $x_{0}$ pontjában van. Jelöljük sebességét $v_{2}$ -vel! Az alábbi egyenletek alakja nem függ attól, milyen irányba mozog a megfigyelő vonat. Ezért elegendő csak az egyik esetet vizsgálni és $v_{2}$ -t előjeles mennyiségként kezelni.
Feltesszük, hogy a második vonat a hangnál lassabban halad. Következésképpen őt a hang utolérheti, másrészt a vezetője nem hallhatja a jelet megszűnni, mielőtt a sípolást az első vonat befejezné. A jel kezdete az $x_{1}$ pontban éri utol a megfigyelőt (1. ábra):

\begin{matrix} \frac{x_{1}}{c} = \frac{x_{1} - x_{0}}{v_{2}} . \end{matrix}

(1)

A sípolást az első vonat az

x_{2} = v_{1} t_{1}

helyen fejezi be, a megfigyelő ekkor az

x_{3} = x_{0} + v_{2} t_{1}

pontban van.

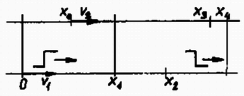1. ábra

Tételezzük fel, hogy

x_{3} ≧ x_{2}

, azaz a két vonat a füttyjel ideje alatt nem haladt el egymás mellett. A jel vége az

x_{4}

helyen éri utol a második vonatot:

\begin{matrix} \frac{x_{4} - x_{2}}{c} = \frac{x_{4} - x_{3}}{v_{2}} . \end{matrix}

(2)

(1) és (2) összevetésével,

x_{2}

-t és

x_{3}

-at beírva, a megfigyelő által észlelt jelhosszúságot megadhatjuk:

\begin{matrix} t_{2} = \frac{x_{4} - x_{1}}{v_{2}} = \frac{c - v_{1}}{c - v_{2}} t_{1}, \end{matrix}

ahonnan

\begin{matrix} v_{2} = c - (t_{1} / t_{2}) (c - v_{1}) = - 27, 69 m/s = - 99, 69 km/h, \end{matrix}

(3)

a vonatok tehát egymással szemben haladnak.
Abban az esetben, ha

x_{3} < x_{2}

, a vonatok a füttyjel alatt elhaladnak egymás mellett. Ekkor (2) helyett

\begin{matrix} \frac{x_{2} - x_{4}}{c} = \frac{x_{4} - x_{3}}{v_{2}} . \end{matrix}

(3)

érvényes. Innen

\begin{matrix} t_{2} = t_{1} \frac{c + v_{1}}{c + v_{2}} - \frac{2 c x_{0}}{c^{2} - v_{2}^{2}}, \end{matrix}

azaz

v_{2}

-re egy másodfokú egyenletet kapunk:

\begin{matrix} v_{2}^{2} t_{2} - v_{2} t_{1} (c + v_{1}) + c (c + v_{1}) t_{1} - c^{2} t_{2} - 2 c x_{0} = 0, \end{matrix}

így

v_{2}

kifejezéséhez a vonatok kezdeti távolságára is szükségünk lenne, azért az eredményt numerikusan nem tudjuk megadni.

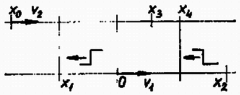2. ábra

A második esetben

x_{0} < 0

(2. ábra). A jel kezdetével a vonat az

x_{1} (< 0)

pontban találkozik:

\begin{matrix} - \frac{x_{1}}{c} = \frac{x_{1} - x_{0}}{v_{2}} . \end{matrix}

(4)

A füttyjel befejeztekor a vonatok az

x_{2} = v_{1} t_{1}

és az

x_{3} = x_{0} + v_{2} t_{1}

pontokban vannak.
Tegyük fel, hogy

x_{3} < x_{2}

, ekkor a jel vége az

x_{4}

pontban találkozik a megfigyelővel:

\begin{matrix} \frac{x_{4} - x_{3}}{v_{2}} = \frac{x_{2} - x_{4}}{c} . \end{matrix}

(5)

A fentiek alapján a megfigyelő

\begin{matrix} t_{2} = \frac{x_{4} - x_{1}}{v_{2}} = t_{1} \frac{c + v_{1}}{c + v_{2}} \end{matrix}

ideig hallotta a sípolást. Innen

\begin{matrix} v_{2} = (t_{1} / t_{2}) (c + v_{1}) - c = 73, 85 m/s = 265, 85 km/h . \end{matrix}

(6)

Amennyiben a vonatok elhaladtak egymás mellett, azaz

x_{2} < x_{3}

, akkor

(5)

helyett

\begin{matrix} \frac{x_{4} - x_{3}}{v_{2}} = \frac{x_{4} - x_{2}}{c} \end{matrix}

(5*)

áll fenn. Ezt felhasználva a fentiekhez hasonlóan számolva

v_{2}

-re a

\begin{matrix} v_{2}^{2} t_{2} + v_{2} (c - v_{1}) t_{1} - c^{2} t_{2} + c (c - v_{1}) t_{1} + 2 c x_{0} = 0 \end{matrix}

egyenletet kapjuk. A

v_{2}

-t megadó képletből

x_{0}

ezúttal nem esik ki, numerikus megoldást ezért nem adhatunk.

Ábrahám Csongor (Kiskunhalas, Szilády Á. Gimn., I. o. t.)

Megjegyzés. Néhány megoldó a leadott, ill. megfigyelt hangot

v_{1} = (1 / 15) 1/s

és

v_{2} = (1 / 13) 1/s

frekvenciájú jelek részének tekintette, s a megfigyelő sebességére a Doppler-effektus képletét írta fel. Ha a megfigyelő kezdeti helyzete felé halad a füttyjelet leadó mozdony, akkor a

\begin{matrix} v_{2} = v_{1} \frac{1 - (v_{2} / c)}{1 - (v_{1} / c)}, \end{matrix}

ha az első pillanatban a megfigyelő az első vonat mögött volt, akkor a

\begin{matrix} v_{2} = v_{1} \frac{1 + (v_{2} / c)}{1 + (v_{1} / c)} \end{matrix}

képletek érvényesek. Ezek az egyenletek a (3), ill. a (6) eredményre vezetnek.
A Doppler-effektust leíró kifejezés feltételezi, hogy egy periódus alatt a jeladó és a megfigyelő nem találkozik. Ezért ez a megközelítés nem tud számot adni arról a fentebb tárgyalt esetről, amikor a füttyjel alatt a vonatok elhaladnak egymás mellett.