Kezdőlap


Feladat:	F.1979	Korcsoport: 18-	Nehézségi fok: -
Megoldó(k):	Bajusz F. , Baksai R. , Bezdek A. , Binzberger G. , Bodó Z. , Déri A. , Fehér J. , Fried M. , Gáti T. , Gelencsér Zsuzsa , Gémes Margit , Homonnay G. , Horváth Erzsébet , Horváth O. , Hujter M. , Husvéti T. , Ivanyos G. , Jónás B. , Kiss b. , Knébel I. , Kóczy Annamária , Koltay K. , Kozma A. , Lovász A. , Lugosi E. , Major Z. , Márkus G. , Nagy I. , Rákos Éva , Réthy I. , Réti Z. , Seress Á. , Soukup L. , Surján P. , Szabó K. , Tornóci L.
Füzet:	1975/december, 206 - 209. oldal		PDF \| MathML
Témakör(ök):	Számsorozatok, Feladat
Hivatkozás(ok):	Feladatok: 1975/március: F.1979

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A sorozat képzési szabálya alapján világos, hogy ha nemcsak $a_{0}$ , hanem még $a_{1}$ értékét is megadjuk, akkor már a sorozat tagjai egyértelműen meg vannak határozva. Nem adhatjuk meg azonban tetszés szerint $a_{1}$ értékét, hiszen $a_{1}$ megválasztásával biztosítanunk kell, hogy a sorozat tagjai pozitívak legyenek. Azt kell megmutatnunk tehát, hogy ez a követelmény $a_{1}$ -et egyértelműen meghatározza.
Jelöljük $a_{1}$ -et $x$ -szel, és nézzük meg $n$ néhány értékére, hogy milyen feltételt jelent $x$ -re az $a_{n} > 0$ alapkövetelmény:

\begin{matrix} \begin{matrix} a_{1} & = x, & tehát & x > 0; \\ a_{2} & = - x + 1, & tehát & x < 1; \\ a_{3} & = 2 x - 1, & tehát & x > \frac{1}{2}; \\ a_{4} & = - 3 x + 2, & tehát & x < \frac{2}{3}; \\ a_{5} & = 5 x - 3, & tehát & x > \frac{3}{5}; \\ a_{6} & = - 8 x + 5, & tehát & x < \frac{5}{8} . \end{matrix} \end{matrix}

Közben megfigyelhettük, hogy

x

együtthatóinak az előjele változik, és ugyanezek az együtthatók lépnek fel a következő tag konstansaként, vagyis

\begin{matrix} a_{n} = {(- 1)}^{n - 1} (λ_{n} x - λ_{n - 1}), \end{matrix}

(1)

ahol

λ_{0} = 0

λ_{1} = 1

λ_{2} = 1

λ_{3} = 2

λ_{4} = 3

λ_{6} = 5

.
Ezekre a számokra teljesül a

\begin{matrix} λ_{n + 1} = λ_{n - 1} + λ_{n} \end{matrix}

(2)

összefüggés, állítsuk elő ennek alapján az egész

λ_{n}

sorozatot. Megmutatjuk, hogy ha a

λ_{n}

sorozatot a

λ_{0} = 0, λ_{1} = 1

kezdőértékek és a (2) összefüggés alapján határozzuk meg, akkor az

a_{n}

sorozat minden tagjára teljesül (1). Már láttuk, hogy (1) igaz

n = 1

2

mellett. Tegyük fel, hogy valamilyen

N ≧ 2

szám mellett már beláttuk, hogy (l) teljesül minden

n ≦ N

indexre. Akkor ebből és a képzési szabályból következik, hogy

\begin{matrix} a_{N + 1} = a_{N - 1} - a_{N} = {(- 1)}^{N - 2} (λ_{N - 1} x - λ_{N - 2}) - {(- 1)}^{N - 1} (λ_{N} x - λ_{N - 1}) = \\ {(- 1)}^{N} (λ_{N - 1} + λ_{N}) x - (λ_{N - 2} + λ_{N - 1})], \end{matrix}

ami (2) alapján valóban (1) alakú.
Mivel

λ_{1} > 0

, (2)-ből következik, hogy

n > 0

mellett

λ_{n} > 0

. Így az

a_{2 k - 1} > 0

feltételből az következik, hogy

x > λ_{2 k - 2} / λ_{2 k - 1}

, az

a_{2 k} > 0

feltételből pedig az, hogy

x < λ_{2 k - 1} / λ_{2 k}

. Jelöljük a

λ_{n - 1} / λ_{n}

hányadost

ξ_{n}

-nel, akkor

\begin{matrix} ξ_{2 k - 1} < x < ξ_{2 k}; k = 1, 2, ... \end{matrix}

(3)

Azt kell megmutatnunk, hogy (3) egyértelműen meghatározza

x

értékét. (2) szerint

\begin{matrix} ξ_{n + 1} = \frac{λ_{n}}{λ_{n + 1}} = \frac{λ_{n}}{λ_{n - 1} + λ_{n}} = \frac{1}{ξ_{n} + 1} . \end{matrix}

A továbbiakban elég ennyit tudnunk a

ξ_{n}

sorozatról, és azt, hogy

ξ_{1} = 0

, hiszen ezzel a

ξ_{n}

sorozat már egyértelműen meg van határozva.

k = 1,2,3

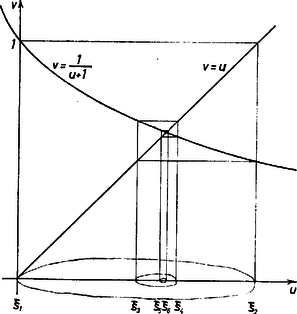számokra (3) rendre a

(0, 1)

(\frac{1}{2}, \frac{2}{3})

(\frac{3}{5}, \frac{5}{8})

nyílt intervallumokat engedi meg

x

szóbajöhető értékeire. Ezek az intervallumok tartalmazzák egymást, szokásos kifejezéssel élve: egymásba vannak skatulyázva. Akárhányat sorolunk is fel közülük, a legutolsó mindig a legrövidebb, benne van mindegyik korábbiban, elég tehát

x

-ről azt megkövetelni, hogy abban legyen benne. (Ezeket az intervallumokat és a

ξ_{n}

sorozat képzési szabályát szemlélteti az ábra.)
Jelöljük az

u = \frac{1}{u + 1}

egyenlet pozitív gyökét

ξ

-vel:

ξ = \frac{1}{2} (\sqrt[]{5} - 1)

. Mivel

\begin{matrix} 0 = ξ_{1} < ξ_{3} < ξ, \end{matrix}

és az

f (u) = \frac{1}{u + 1}

függvény

u ≧ 0

mellett monoton fogy,

\begin{matrix} f (ξ_{1}) > f (ξ_{3}) > f (ξ), \end{matrix}

azaz

\begin{matrix} ξ < ξ_{4} < ξ_{2} . \end{matrix}

Hasonlóan a

\begin{matrix} 0 \leq ξ_{2 k - 1} < ξ_{2 k + 1} < ξ \end{matrix}

egyenlőtlenségből a

\begin{matrix} ξ < ξ_{2 k + 2} < ξ_{2 k} \end{matrix}

egyenlőtlenséget kapjuk, ebből pedig a

\begin{matrix} 0 ≦ ξ_{2 k + 1} < ξ_{2 k + 3} < ξ \end{matrix}

egyenlőtlenséget. Tehát a

ξ_{n}

sorozat páratlan indexű tagjaiból álló részsorozata monoton nő, és a tagok kisebbek

ξ

-nél, a páros indexű tagok részsorozata pedig monoton fogy, és a tagok nagyobbak

ξ

-nél. Emiatt (3) teljesül az

x = ξ

számra, azt kell még megmutatnunk, hogy másra nem teljesülhet. Tudjuk, hogy

\begin{matrix} δ_{k} = ξ_{2 k} - ξ_{2 k - 1} \end{matrix}

sorozat monoton fogy és tagjai pozitívak. Megmutatjuk, hogy ez a sorozat

0

-hoz tart. Ebből már következik állításunk, hiszen ha volna olyan

x \neq ξ

szám, amelyre teljesülne (3), akkor a

δ_{k}

sorozat minden tagja nagyobb volna a pozitív

| ξ - x |

-nél, ami

δ_{k} \to 0

miatt nem lehet. Mivel

\begin{matrix} δ_{k} = ξ_{2 k} - ξ_{2 k - 1} = \frac{λ_{2 k - 1}}{λ_{2 k}} - \frac{λ_{2 k - 2}}{λ_{2 k - 1}} = \frac{λ_{2 k - 1}^{2} - λ_{2 k} λ_{2 k - 2}}{λ_{2 k} λ_{2 k - 1}}, \end{matrix}

készen is vagyunk, ha belátjuk, hogy itt a számláló értéke mindig

1

, hiszen a nevező a nyilvánvaló

λ_{n} ≧ n

egyenlőtlenség miatt tart végtelenbe. A

Δ_{n} = λ_{n}^{2} - λ_{n - 1} λ_{n + 1}

sorozat tagjaira

\begin{matrix} Δ_{n + 1} = λ_{n + 1}^{2} - λ_{n} λ_{n + 2} = λ_{n + 1}^{2} - λ_{n} (λ_{n} + λ_{n + 1}) = λ_{n + 1} (λ_{n + 1} - λ_{n}) - λ_{n}^{2} = \\ λ_{n + 1} λ_{n - 1} - λ_{n}^{2} = - Δ_{n} \end{matrix}

teljesül, tehát

Δ_{n + 2} = Δ_{n}

, így

Δ_{1} = 1

miatt a sorozat minden páratlan indexű tagja

1

-gyel egyenlő. Mivel

δ_{k}

fenti alakjában éppen ezek állnak a számlálóban, a bizonyítást ezzel befejeztük.

Megjegyzés. Általában ha egy

ξ_{n}

sorozatról tudjuk, hogy a páratlan indexű tagjainak részsorozata monoton nő, a páros indexűeké pedig fogy, és a

δ_{k} = ξ_{2 k} - ξ_{2 k - 1}

különbség

0

-hoz tart, akkor a sorozat konvergens. A megoldók többsége erre az állításra hivatkozva bizonyította, hogy a (3) feltételnek egy és csakis egy megoldása van. Ebből a "csak egy'' rész a

δ_{k} \to 0

feltétel következménye, mint azt megoldásunkban is láttuk, a "legalább egy'' rész pedig szervesen kapcsolódik a valós szám fogalmához. Tekintve, hogy az analízis alapfogalmainak jelenleg használt középiskolai bevezetése nagymértékben támaszkodik a szemléletre, ez a tétel nem szerepel a tananyagban, ezért bizonyítottuk a (3) feltételnek eleget tevő

x

szám létezését e tétel felhasználása nélkül (ami különben nem került különösebb fáradságba, hiszen ez az

x

az esetünkben explicit megadható volt).