Feladat: F.1970 Korcsoport: 18- Nehézségi fok: -
Füzet: 1975/december, 205 - 206. oldal  PDF  |  MathML 
Témakör(ök): Gömbi geometria, Bolyongási feladatok, Feladat
Hivatkozás(ok):Feladatok: 1975/január: F.1970

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük az absztrakt állatot A-val, kiindulópontját P-vel, a gömb középpontját O-val, soron következő lépéseinek végpontját Q-val, R-rel, S-sel. Mivel egy lépés hossza kisebb a gömb átmérőjénél, A-nak mindig van hova lépnie. Feltevésünk szerint R nem lehet P-vel azonos, megmutatjuk, hogy S sem lehet az. Ellenkező esetben ugyanis a PQR háromszög minden oldala 1,99 volna, és ez nagyobb az egységsugarú gömbbe írható legnagyobb szabályos háromszög oldalánál, 3-nál. A-nak tehát legalább négyet kell lépnie, és mint látni fogjuk, ha kicsit is óvatos, négy lépéssel már visszajuthat 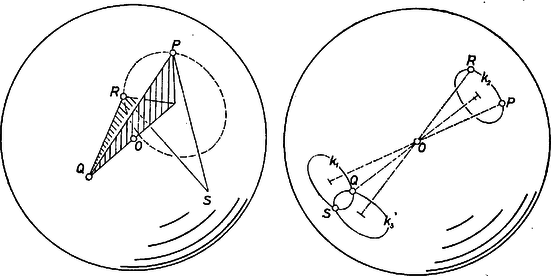P-be.

 

 

Ha A négy lépésben vissza akar jutni P-be, első lépése még tetszőleges lehet. Második lépésében csak arra kell ügyelnie, hogy R ne legyen benne az OPQ síkban. Forgassa el mondjuk 90∘-kal P-t az OQ tengely körül, akkor a kapott R pontra QR=QP, és az OQP, OQR síkok merőlegesek lesznek, ebbe az R-be nyugodtan léphet A. Tükrözze ezután A az OPR síkra Q-t, és legyen S a kapott tükörkép. Mivel Q nincs benne az OPR síkban (hiszen R nincs benne az OPQ síkban), S a P, Q, R pontok mindegyikétől különböző lesz, és RS=RQ miatt ide léphet A R-ből, SP=QP miatt pedig innen már visszajuthat P-be. Ezzel beláttuk, hogy A legrövidebb körsétája négy lépésből áll.
 

II. megoldás. Az első lépésben arra a k1 körre léphet A, melynek pontjai P-től 1,99 egységnyire vannak, és amelyet a P-n átmenő gömbátmérőre merőleges sík metsz ki a gömbből. Ha négy lépésben vissza akar érni P-be, akkor harmadik lépésben ismét ennek a körnek egy pontjára kell lépnie.
Az első lépésben k1 bármelyik Q pontjába léphet. A második lépéssel elérhető pontok a P-n átmenő, k1-gyel egybevágó k2 kör pontjai, amelyiknek síkja a Q-n átmenő gömbátmérőre merőleges.
Hasonlóan k2 valamely, a P-től különböző R pontjából a Q-n átmenő, k1-gyel egybevágó, de attól különböző k3 körre léphet A. Az S pontnak rajta kell lennie k1-en is, k3-on is és különböznie kell Q-tól. Ilyen pont csak akkor nincs, ha k1 és k3 érintkezik Q-ban; ez viszont akkor következik be, ha R a k2 P-vel átellenes pontja.
Azt kaptuk tehát, hogy ha A második lépésben a k2 kör P-től és a vele átellenes ponttól különböző R pontjába lép, akkor mindig van egy egyértelműen meghatározott S pont a gömbön, ti. k1 és k3 kör Q-tól különböző metszéspontja, amelyikre lépve harmadszorra, negyedik lépéssel visszaérhet P-be.