Kezdőlap


Feladat:	1570. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: -
Megoldó(k):	Bodó Zalán , Bokor József , Cseke István , Győri Erzsébet , Honos Attila , Horváth József (Szhely) , Hunyady László , Kamondi Zoltán , Knébel István , Kruchió Gábor , Lendvay András , Márkus Zoltán , Nagy Lajos (Szhely) , Rábai Zoltán , Rapai Tibor , Ságody Lőrinc , Székely Zoltán , Verő Mária
Füzet:	1975/december, 215 - 216. oldal		PDF \| MathML
Témakör(ök):	Kombinatorikai leszámolási problémák, Elsőfokú (és arra visszavezethető) egyenletrendszerek, Gyakorlat
Hivatkozás(ok):	Feladatok: 1975/március: 1570. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ha az ábra $20$ körének mindegyikébe $0$ -t írunk, akkor teljesül a feltétel. Azt akarjuk megmutatni, hogy másképp nem is lehet kitölteni az ábrát: ha a beírt számokra a feltétel teljesül, úgy mindenhová $0$ -t kellett írnunk.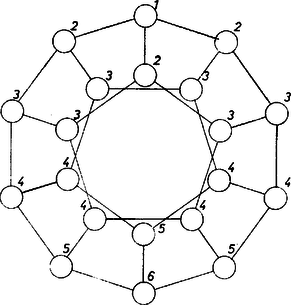

Vegyük észre, hogy az ábra "forgásszimmetrikus'', középpontja körül

360^{\circ} / 10 = 36^{\circ}

-kal elfordítva önmagába megy át. Így, ha sikerül megmutatnunk, hogy a külső vonal egy meghatározott (pl. a kis

1

-essel jelölt) körébe

0

-t kell írnunk, akkor ebből már következik, hogy a külső vonal minden körébe

0

-t kell írnunk. És ha még azt is megmutatjuk, hogy a belső körök egyikébe (pl. a

2

-es jelűbe) is

0

-t kell írnunk, ezzel azt is igazoljuk, hogy az ábra minden köre csak

0

-t tartalmazhat. Hiszen ha egy megoldásban volna olyan kör, amelyben nem

0

van, azt elforgatással átvihetnénk vagy az

1

-es vagy a

2

-es jelű körbe, a beírt számokra pedig továbbra is áll a feltétel.
Jelöljük az

i

-vel jelölt körökben álló számok összegét

a_{i}

-vel

(i = 1,2, ... 6)

, és írjuk fel egymás után minden

i

-re az összes

i

-vel jelölt körökre a feltételek összegét. Így a következő

6

egyenletet kapjuk:

\begin{matrix} \begin{matrix} a_{i} + a_{2} = 0; & 3 a_{1} + a_{2} + a_{3} = 0; & 2 a_{2} + 2 a_{3} + a_{4} = 0; \\ a_{3} + 2 a_{4} + 2 a_{5} = 0; \end{matrix} \end{matrix}

(Pl. a

3

2

-es jelű kör feltételeinek összegében

3 \cdot 4 = 12

tag szerepel, az

1

-es kör száma

3

-szor, a

3

2

-es

1

-szer‐

1

-szer és ugyanígy a

6

3

-as is, mert mindegyik

2

-es az

1

-essel és

2 - 2

3

-assal szomszédos, mindegyikük másik

2

3

-assal.) Az elsőből

a_{2}

-t, a másodikból

a_{3}

-t,

...

, az ötödikből

a_{6}

-t fejezzük ki

a_{1}

segítségével:

a_{2} = - a_{1}

;

a_{3} = - 2 a_{1}

;

a_{4} = 6 a_{1}

;

a_{5} = - 5 a_{1}

;

a_{6} = - a_{1} / 3

. Ezt a hatodikba helyettesítve kapjuk, hogy

a_{1} = 0

, vagyis az

1

-es jelű körbe valóban

0

-t kell írnunk.
Az előrebocsátottak szerint ekkor a külső vonal mindegyik köre

0

-t tartalmaz, tehát az

1

-es körre a feltétel csak úgy állhat ‐ mivel a szóban forgó négy kör közül három a külső vonalon van ‐, ha a belső

2

-es körben is

0

áll.
Ezzel állításunkat bebizonyítottuk.

Megjegyzések. 1. A megoldók többsége a

20

körbe írt számokat

20

ismeretlennek fogta fel, a feltételeket pedig

20

egyenletnek, majd megmutatta (több-kevesebb ügyeskedéssel), hogy az egyenletrendszer egyetlen megoldása az, amikor mindegyik ismeretlen

0

. Volt, aki kiküszöböléssel, rengeteg számolás árán jutott el az eredményig. A hibás dolgozatok egy része hivatkozott az ún. Cramer-szabályra, amely az ilyen típusú egyenletrendszerek megoldására szolgál, de a feladat állításával ekvivalens állítást, hogy ti. a rendszer

20 \times 20

-as determinánsának értéke nem nulla, legfeljebb "megemlítették'', de egyikük sem bizonyította. A fenti megoldásból ez egyébként következik.

2. Az ábra tekinthető egy szabályos dodekaéder (

12

szabályos ötszöglappal határolt konvex test) élváza merőleges vetületének egy lap síkjára. (A körök a csúcsokat jelentik, a körök akkor vannak összekötve, ha a megfelelő csúcsok között él fut.) Ebben a felfogásban a testet úgy forgathatjuk különböző tengelyei (lap-, él- és csúcstengelyek) körül, hogy a test önmagával fedésbe jusson és tetszőleges csúcsa tetszőleges másik csúcsa helyére jusson; eszerint az ábra külső és belső körei is egyenrangúak.