Kezdőlap


Feladat:	1580. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: -
Füzet:	1975/november, 146 - 147. oldal		PDF \| MathML
Témakör(ök):	Háromszögek nevezetes tételei, Súlyvonal, Gyakorlat
Hivatkozás(ok):	Feladatok: 1975/április: 1580. matematika gyakorlat

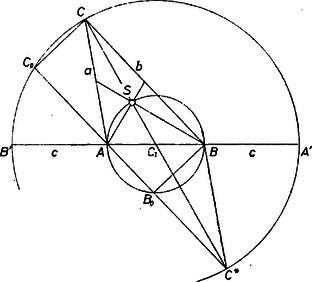
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyenek az $A B C$ háromszögnek az $A$ és $B$ csúcsából kiinduló súlyvonalai merőlegesek egymásra. Így közös pontjukból, az $S$ súlypontból az $A B$ oldalt derékszögben látjuk, $S$ rajta van az $A B$ átmérőjű Thalész-kör kerületén, tehát $S$ -nek az $A B = c$ oldal $C_{1}$ felezőpontjától való távolsága egyenlő az oldal felével: $S C_{1} = A B / 2$ . És mivel $S$ harmadolja a $C_{1} C$ súlyvonalat, azért $C_{1} C = 3 A B / 2$ , vagyis $C$ rajta van a $C_{1}$ körüli $s_{c} = 3 c / 2$ sugarú körön. ‐ Meggondolásunk megfordítható, a feltétel tehát nemcsak szükséges, hanem elégséges is.

C C_{1} = s_{c}

súlyvonal bármely háromszögben egyszerűen kifejezhető a három oldallal, így az előbbi helyzetfeltételt átalakíthatjuk a háromszög oldalai közti méretes feltétellé. Legyen

C

tükörképe

C_{1}

-re

C^{*}

, ekkor a

C A C^{*} B

paralelogramma átlói és oldalai között fennáll:^{$^{*}$}

\begin{matrix} C C^{* 2} + A B^{2} & = A C^{2} + C B^{2} + B C^{* 2} + C^{*} A^{2}, \\ 4 s_{c}^{2} + c^{2} & = 2 a^{2} + 2 b^{2} . \end{matrix}

Ez esetünkben a feltétel a talált

2 s_{c} = 3 c

alakja alapján így specializálódik:

\begin{matrix} 5 c^{2} = a^{2} + b^{2}, \end{matrix}

(1)

és ez ugyancsak szükséges és elegendő az

a

b

c

oldalakkal meghatározott háromszög

a

és

b

oldalaihoz tartozó súlyvonalak merőlegességéhez.

Megjegyzés. Abból, hogy a vizsgált háromszögekben

C

rajta van a

C_{1}

körüli

3 c / 2 = 3 \cdot {A C}_{1} = 3 B C_{1}

sugarú körön, következik, hogy a további két oldal nagyságra nézve

c

és

2 c

közé esik:

c < a

b < 2 c

, hiszen a körnek az

A B

egyenesen levő,

A

-hoz legközelebbi

B'

és

A

-tól legtávolabbi

A'

pontjára

B' A = A B = B A' = c

A A' = 2 c

, és ha

C

egybeesnék

B'

-vel,

A'

-vel, akkor már nem jönne létre valódi háromszög.
Mégsem kell a talált

(1)

feltétel mellé még azt is kikötnünk, hogy

c

a háromszög legrövidebb oldala legyen. Ha ugyanis pl.

a = ϑ c

lenne, ahol

0 < ϑ \leq 1

akkor

(1)

-ből

\begin{matrix} b^{2} = (5 - ϑ^{2}) c^{2} \geq 4 c^{2}, b \geq 2 c, \end{matrix}

és ekkor

a

b

c

oldalakkal nem szerkeszthető háromszög, mert nem teljesül a háromszög-egyenlőtlenség, hiszen

b \geq a + c

^{$^{*}$}A felhasznált segédtételt úgy kapjuk, hogy Pitagorasz tételét alkalmazzuk a

C C^{*} C_{0}

A B B_{0}

A C C_{0}

B C^{*} B_{0}

derékszögű háromszögekre, ahol

B_{0}

C_{0}

B

C

csúcs vetülete az

A C^{*}

egyenesen.