Feladat:	1575. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: -
Megoldó(k):	Jónás Béla
Füzet:	1975/november, 142 - 144. oldal		PDF  |  MathML
Témakör(ök):	Háromszögek nevezetes tételei, Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1975/március: 1575. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. $\begin{array}{c}{\displaystyle b{c}^2=\left(a+b\right){\left(a-b\right)}^2\mathrm{.}}\end{array}$ (1) I. megoldás. A feltevések szerint $\beta =2\gamma$ és $\alpha =6\gamma$, tehát a szögek összegéből $\gamma ={20}^{\circ }$, majd $\beta ={40}^{\circ }$, $\alpha ={120}^{\circ }$. Fordítsuk rá $C$ körül $A$-t a $CB$ félegyenesre $A_1$-be és $B$-t a $CA$-ra, $B_1$-be, továbbá $A$ körül $B$-t a $BC$-re, a $B_2$ pontba (1. ábra). 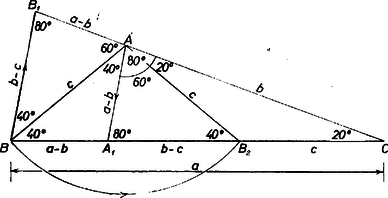    1. ábra   Így $CA{A}_1$, $CB{B}_1$, $AB{B}_2$ egyenlő szárú háromszögek, az ezekből kiadódó szögértékek alapján egyszerű számítás szerint a $B_{2}CA$ és $A_{1}AB$ háromszög is egyenlő szárú: $B{B}_{2}A\sphericalangle ={40}^{\circ }$, a külső szög tétele alapján $B_{2}AC\sphericalangle ={40}^{\circ }-\gamma ={20}^{\circ }=\gamma$, illetve $C{A}_{1}A\sphericalangle ={80}^{\circ }$, $A_{1}AB\sphericalangle ={80}^{\circ }-\beta ={40}^{\circ }=\beta$. Továbbá az $AB{B}_1$ és $A{B}_2{A}_1$ háromszögek szögei (a csúcsok felsorolásának rendjében) páronként egyenlők: ${60}^{\circ }$, ${40}^{\circ }$, ${80}^{\circ }$. A szerkesztésünk és számításunk szerint egyenlő szakaszok: $B{A}_1=B_{1}A=A{A}_1=a-b$ és $AB=A{B}_2=B_{2}C=c$, így az $AB{B}_1$ és $A{B}_2{A}_1$ háromszögek egybevágóak, ezért $B_{1}B=A_1{B}_2=C{A}_1-C{B}_2=b-c$, továbbá $B{B}_2=a-c$. Mármost a $CA{A}_1$, $C{B}_{1}B$, majd az $AB{B}_2$, $A_{1}AB$ háromszögpárok hasonlósága alapján, megfelelő oldalpárjaik arányából $\begin{array}{c}{\displaystyle \frac{a-b}{b-c}=\frac{b}{a}\mathrm{,}\text{illetve}\frac{a-c}{c}=\frac{c}{a-b}\mathrm{.}}\end{array}$ Ezekből ‐ egy kis előrelátó ügyeskedéssel ‐ az $\left(1\right)$ bal oldalának tényezőire a következőket írjuk fel: $\begin{array}{c}{\displaystyle b=\frac{a^2-b^2}{a-c}\mathrm{,}\text{illetve}{c}^2=\left(a-c\right)\left(a-b\right);}\end{array}$ innen ugyanis a jobb oldalak szorzata azonnal egyenlőnek adódik az $\left(1\right)$ jobb oldalával. Ezzel az állítást bebizonyítottuk.   Megjegyzés. Az $ABC$ háromszög köré írt $k$ körből az $AB$, $BC$, $CA$ oldal által lemetszett ív a középpontból rendre $2\gamma ={40}^{\circ }$, $2\alpha ={240}^{\circ }=6\cdot {40}^{\circ }$, $2\beta =2\cdot {40}^{\circ }$ szögben látható. És mivel ${40}^{\circ }$-os középponti szög tartozik a $k$-ba beírt $1+6+2=9$ oldalú szabályos sokszög oldalaihoz is, azért $A$, $B$ és $C$ annak a szabályos $9$-szögnek a csúcsai közül valók, amelynek oldalhossza $c$; ekkor egy csúcsát a tőle második, illetve harmadik csúccsal összekötő átló hossza $b$, ill. $a$.   II. megoldás. Ha a fentieknél kissé több számítást engedünk meg magunknak, és felhasználjuk a hegyesszög cosinusának definícióját, akkor $\left(1\right)$ bizonyításához elég a feltevésnek az $\alpha =3\beta$ része. Az $\alpha +\beta <{180}^{\circ }$ kapcsolat miatt természetesen $\beta <{45}^{\circ }$. (Valóban, $\beta ={30}^{\circ }$ és $b=1$ mellett $a=2$, $c=\sqrt[]{3}$, és teljesül az állítás.) Mérjük fel ismét $CA$-t a $CB$ félegyenesre: $CD=CA$, így $D$ a $CB$ szakaszon van, hiszen $\alpha >\beta$ miatt 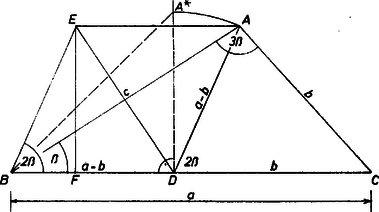$a>b$, azaz $CB>CA$ (2. ábra).     2. ábra   Mivel $\gamma ={180}^{\circ }-4\beta$, azért $CAD\sphericalangle =CDA\sphericalangle =2\beta$, tehát $DAB\sphericalangle =\beta =DBA\sphericalangle$, ennélfogva $DA=DB=a-b$. Így a $CAD$ és a $DAB$ háromszögből. $\begin{array}{c}{\displaystyle \text{cos}2\beta =\frac{a-b}{2b}\mathrm{,}\text{illetve}\text{cos}\beta =\frac{c}{2\left(a-b\right)}\mathrm{.}}\end{array}$ (2) Legyen még $D$-nek $AB$-re való tükörképe $E$, és $E$-nek $BD$-n levő vetülete $F$. Ekkor $EBD\sphericalangle =2\beta$, és a $BEAD$ rombusz területének kétféle kifejezéséből ${\displaystyle \begin{array}{c}\hfill {\displaystyle EF=\frac{AB\cdot DE}{2BD}=\frac{AB}{BD}\sqrt[]{B{D}^2-\frac{A{B}^2}{4}}\mathrm{,}}\hfill \\ \hfill {\displaystyle B{F}^2=B{E}^2-E{F}^2=B{E}^2-A{B}^2+\frac{A{B}^4}{4B{D}^2}=}\hfill \\ \hfill {\displaystyle =\frac{1}{4{\left(a-b\right)}^2}\left\{c^4-4c^2{\left(a-b\right)}^2+4{\left(a-b\right)}^4\right\}\mathrm{,}}\hfill \\ \hfill {\displaystyle \text{cos}2\beta =\frac{BF}{BE}=\frac{c^2-2{\left(a-b\right)}^2}{2{\left(a-b\right)}^2}=2{\left(\frac{c}{2\left(a-b\right)}\right)}^2-1.}\hfill & \text{(<mn>3</mn>)}\end{array}}$ A négyzetgyök előjelét helyesen vettük, mert $\beta <{45}^{\circ }$ miatt $BA>B{A}^{*}$, ahol $A^{*}$ az $A$ ráforgatottja a $D$-ben emelt merőlegesre, tehát $c>\sqrt[]{2}\left(a-b\right)$. A bal oldalon $\left(2\right)$ első kifejezését helyettesítve, kellő alakítás után $\left(1\right)$-et kapjuk.     Jónás Béla (Budapest, Berzsenyi D. Gimn., III. o. t.)   Megjegyzések. 1. Ennek a bizonyításnak az ötlete abból adódhat, ha valaki megpróbálja megfordítani a tételt. Az $\left(1\right)$ összefüggés feltevéséből azonban már eleve nem várható, hogy két kapcsolatot kapjunk a szögek között. A megfordítás így hangzik: ha egy háromszögben fennáll $\left(1\right)$, akkor $\alpha =3\beta$. Ez több geometriai számítással igazolható. A dolgozatok jelentős részében az eredeti feltevés melletti bizonyításnak is geometriai azonosságok az eszközei. 2. $\left(3\right)$ jobb oldalába $\left(2\right)$ második kifejezését írva, a goniometriából ismert $\text{cos}2\beta =2\text{cos}{}^2\beta -1$ azonosságot kapjuk, de csak a $0^{\circ }<\beta <{45}^{\circ }$ korlátozással.