Kezdőlap


Feladat:	1568. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1975/november, 139. oldal		PDF \| MathML
Témakör(ök):	Egyenlőtlenségek, Síkgeometriai bizonyítások, Derékszögű háromszögek geometriája, Oldalak aránya és szögek közötti kapcsolat, Gyakorlat
Hivatkozás(ok):	Feladatok: 1975/február: 1568. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Messe az $O$ csúcsú, $x$ nagyságú hegyesszög szárait az $O$ körüli egységnyi sugarú kor az $A$ , $B$ pontokban, a kör $A$ -beli érintője az $O B$ félegyenest $C$ -ben, és legyen $B$ vetülete az $O A$ szakaszon 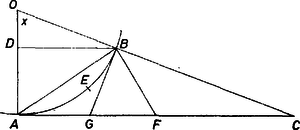$D$ .

Így az állítás

\begin{matrix} \frac{\hat{A B}}{O A} < \frac{1}{2} (\frac{D B}{O B} + \frac{A C}{O A}) = \frac{D B + A C}{2 \cdot O A}, \end{matrix}

mi pedig azt az egyenlőtlenséget bizonyítjuk, amely ebből

O A^{2} / 2

-vel való szorzás útján áll elő, tehát egyenértékű vele. A szorzatokat mindjárt a körcikk, illetve egy-egy háromszög területeként értelmezve, és a területeket az idom lényeges pontjaival jelölve (

E

A B

ív tetszőleges belső pontja), ezt mutatjuk meg:

\begin{matrix} O A E B < \frac{1}{2} (O A B + O A C) = \frac{1}{2} (2 \cdot O A B + A B C) = \\ = O A B + \frac{A B C}{2} = O A B + A B F = O A F B, \end{matrix}

ahol

F

A C

érintőszakasz felezőpontja.
Elég azt belátnunk, hogy az

O A F B

négyszög mindig tartalmazza az

O A B

körcikket, vagyis hogy a

B F

szakasz az

x

-nek egyetlen

0

és

π / 2

közti értéke mellett sem metszi át a

B A

ívet. Messe a kör

B

-beli érintője

A C

-t

G

-ben. Így a

G C B

derékszögű háromszögből

\begin{matrix} G C > G B = G A, \end{matrix}

mindkét oldalt

A G

-vel növelve, majd

2

-vel osztva,

\begin{matrix} \frac{A C}{2} = A F > A G, \end{matrix}

vagyis

F

kívül van az

A G

szakaszon. Ez bizonyítja állításunkat.