Kezdőlap


Feladat:	1548. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: -
Megoldó(k):	Bátky Zsolt , Binzberger Gábor , Brindza Béla , Cservenka Péter , Csúri Miklós , Füle György , Fürbusz Ferenc , Gyenes László , Hibbey Csaba , Horváth László , Incze Gabriella , Juhász Jenő , Kácsor József , Kappelmayer Gábor , Kiss Sándor , Kun Márta , Miklós László , Nagy István , Neumer Attila , Piszkor Loránd , Rábai Zoltán , Specker Attila , Szabó Kálmán , Szabó Sándor , Tankovics Tibor , Unger János , Váczi Zoltán
Füzet:	1975/november, 131 - 132. oldal		PDF \| MathML
Témakör(ök):	Sakktáblával kapcsolatos feladatok, Gyakorlat
Hivatkozás(ok):	Feladatok: 1974/november: 1548. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Mivel a sakktáblán $32$ fehér mező van, azért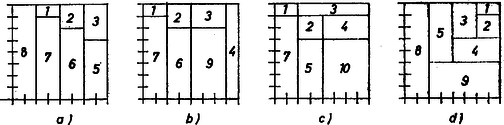

\begin{matrix} a_{1} + a_{2} + ... + a_{p} = 32. \end{matrix}

Innen következik, hogy

p

legfeljebb

7

lehet, hiszen a b) feltétel szerint

p \geq 8

esetén

\begin{matrix} a_{1} + a_{2} + ... + a_{p} \geq 1 + 2 + ... + 8 = 36 > 32. \end{matrix}

Meg kell vizsgálnunk, hogy

p = 7

lehetséges-e. Több-kevesebb próbálkozás után találunk a feladat feltételeinek megfelelő szétvágást, ilyet láthatunk az ábra a) részén. Ezzel válaszoltunk a feladat első felére:

p

legnagyobb értéke

7

.
Ahhoz, hogy az összes lehetséges,

p = 7

értékhez tartozó sorozatot előállítsuk, nézzük meg, az

a_{1}, ..., a_{7}

számok között milyen számok szerepelhetnek?

1 - 10

-ig bármely szám szerepelhet.

11

nem, hiszen

11 \cdot 2 = 22

négyzetből álló téglalapot

8 \times 8

-as négyzetből nem lehet kivágni.

11

-nél nagyobb sem szerepelhet, hiszen ekkor a többi hat különböző természetes szám összege legfeljebb

32 - 12 = 20

lehetne, viszont

1 + 2 + ... + 6 = 21

.
A

8

9

10

számok közül legalább egynek szerepelnie kell, hiszen az első

7

természetes szám összege csak

28

. A

8

-as és

10

-es vagy a

9

-es és

10

-es egyszerre nem szerepelhet, mivel a többi öt különböző tag összegének

14

-nek illetve

13

-nak kellene lennie, ami nem lehet, mert

1 + 2 + 3 + 4 + 5 = 15

. Attól függően, hogy a

8

9

10

számok közül melyek szerepelnek, négy lehetséges esetünk marad:

a) csak a

8

-as szerepel:

1 + 2 + ... + 8 = 36

, ezek közül egyet kell elhagynunk, hogy a megmaradó hét összege

32

legyen. Ezt csak a

4

-es eltörlésével kaphatjuk meg. Ekkora sorozat:

1

2

3

5

6

7

8

.
b) csak a

9

-es szerepel: Ugyanúgy, mint az előbb, az

5

-öt törölve kapjuk az

1

2

3

4

6

7

9

sorozatot.
c) csak a

10

-es szerepel: a

6

-ost törölve kapjuk az

1

2

3

4

5

7

10

sorozatot.
d) a

8

-as és

9

-es együtt szerepel. Az

1

2

...

8

9

számok közül kettőt kell törölnünk, hogy az összeg

45 - 32 = 13

-mal csökkenjen, de a

8

-ast és a

9

-est meg kell hagynunk. Ezt csak a

6

-os és

7

-es törlésével érhetjük el, így a sorozat:

1

2

3

4

5

8

9

Ezek szerint a

p = 7

értékhez legfeljebb a fenti négy sorozat tartozhat. Hátra van még annak megmutatása, hogy ezeket a sorozatokat feldarabolással valóban meg is kaphatjuk. Mindegyik sorozathoz látható egy-egy feldarabolás az ábrán.

Neumer Attila (Budapest, Fazekas M. Gyak. Gimn., I. o. t.)