Kezdőlap


Feladat:	F.1988	Korcsoport: 18-	Nehézségi fok: -
Megoldó(k):	Bezdek A. , Brindza B. , Déri A. , Gáti T. , Hídvégi Z. , Honos A. , Horváth Á. , Horváth Erzsébet , Horváth O. , Husvéti T. , Jakab T. , Koller Gy. , Koltay K. , Láng Gy. , Lugosi Erzsébet , Major Zoltán , Márkus G. , Nagy Imre , Nagy László , Pancsovay R. , Soukup L. , Stark G. , Surján P. , Szabó Illés , Szabó Kálmán , Unger J. , Vancsó Ö.
Füzet:	1975/november, 129 - 131. oldal		PDF \| MathML
Témakör(ök):	Ellipszis egyenlete, Mértani helyek, Ellipszis, mint kúpszelet, Feladat
Hivatkozás(ok):	Feladatok: 1975/április: F.1988

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. 1. Legyen az $A B C$ háromszög $A B$ oldala az adott $e_{1}$ ellipszis nagytengelye, $C$ csúcsa az $e_{1}$ tetszőleges pontja, $A$ és $B$ kivételével, és a háromszög magasságpontja $M$ . Ekkor a $C M$ magasságvonal az $A B$ egyenest egy az $A$ és $B$ közti $C_{0}$ pontban metszi, $C A C_{0}$ és $C B C_{0}$ hegyesszögek. Jelöljük $k$ -val az $A B = 2 a$ szakasz mint átmérő fölötti Thalész-kört, $D$ -vel $k$ -nak a $C_{0} C$ félegyenesen levő pontját és $2 b$ -vel ellipszisünk kistengelyének hosszát. Ekkor minden egyes $C$ pont a belőle származtatott $D$ -nek a képe abban a merőleges affinitásban (összenyomásban), melynek tengelye az $A B$ egyenes, arányszáma a $b / a = λ$ szám, amelyre 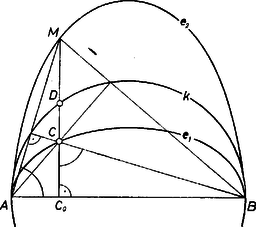$0 < λ \leq 1$ .

Mivel

M A ⊥ B C

, azért az

M A C_{0}

és

B C C_{0}

szögek ‐ mint merőleges szárú hegyesszögek ‐ egyenlők; másrészt nyilván

A D ⊥ D B

. Előbb az

M A C_{0}

B C C_{0}

, majd a

B D C_{0}

D A C_{0}

derékszögű háromszögpár hasonlósága alapján

\begin{matrix} \frac{M C_{0}}{A C_{0}} = \frac{B C_{0}}{C C_{0}} = \frac{B C_{0}}{λ \cdot D C_{0}} = \frac{1}{λ} \cdot \frac{D C_{0}}{A C_{0}}, \end{matrix}

amibő1

\begin{matrix} M C_{0} = \frac{1}{λ} \cdot {D C}_{0} = \frac{a}{b} \cdot {D C}_{0} . \end{matrix}

Eszerint az

M

pont a

D

-ből

a / b (\geq 1)

arányú nyújtással származik. Ezzel tulajdonképpen azt is kimondtuk, hogy

M

ugyanazon a partján van

A B

-nek, mint

C

, ezt azonban még igazolnunk kell. Valóban,

C

k

belsejében van, ezért az

A C B

szög tompaszög, és így az

A

-ból,

B

-ből induló magasságvonalak az

A C B

szög csúcsszögtartományában metszik egymást.
Mivel

C

előírt mozgása folyamán

D

bejárja

k

-nak minden pontját, azért

M

mindig rajta van a

k

-ból az

A B

tengelyű,

a / b

arányszámú nyújtással származó vonalon (magát

A

-t és

B

-t természetesen kivéve). Fordítva, ennek a vonalnak bármely

M^{*}

pontja előáll egy

A B C^{*}

háromszög magasságpontjaként, ehhez

C^{*}

-ot az

M^{*}

-ból

A B

-re bocsátott merőleges metszi ki

e_{1}

-ből,

A B

-nek az

M^{*}

-ot tartalmazó partján. A keresett mértani hely tehát a

k

kör képe a mondott nyújtásban. ‐ Ez nyilvánvalóan egy

e_{2}

ellipszis, amelynek kistengelye az

A B

szakasz, nagytengelye

A B \cdot (a / b) = 2 a^{2} / b

. ‐ Mivel így

e_{2}

-ben a szimmetriatengelyek aránya ugyanaz, mint

e_{1}

-ben, azért ezt is mondhatjuk:

M

mértani helye forgatva nyújtással áll elő

e_{1}

-ből, a forgatás szöge

90^{\circ}

, a nyújtás aránya

a / b

, de

A

és

B

nem tartozik hozzá a mértani helyhez. Még másképpen: mivel

k

e_{1}

-ből és

e_{2}

is a

k

-ból

(a / b)

arányú (és ugyanazon irányú) nyújtással keletkezik, azért ‐ a

k

kör közvetítő szerepét kiiktatva ‐ :

e_{2}

e_{1}

ből az

A B

-re merőleges,

{(a / b)}^{2}

arányú nyújtással áll elő.
2. Azt az esetet, ha a beírt háromszög rögzített oldala az adott ellipszis kistengelye, visszavezethetjük eredményünkre, annak figyelembevételével, hogy ha az

A B C

háromszög magasságpontja

M

, akkor az

A B M

háromszög magasságpontja

C

. Valóban,

e_{2}

-t tekintve adottnak, és ha

A B M

e_{2}

-be beírt háromszög, aho1

A B

e_{2}

-nek kistengelye. Így pedig

C

e_{1}

-et írja le, ami a kistengely mint átmérő fölötti Thalész-kör képe abban az affinitásban, melynek tengelye

e_{2}

kistengelye, arányszáma pedig a rögzített oldal és a rá merőleges szimmetriatengely aránya. ‐ Az arányszám ilyen értelmezése mellett az eredménynek a fenti, forgatva-nyújtásos származtatása ebben az esetben is érvényes.
3. Az

a = b

, azaz

λ = 1

esetben

e_{1}

körré (

k

-vá) specializálódik, nincsenek kiemelt szimmetriatengelyek,

e_{2}

azonos

e_{1}

-gyel. Ez a semmitmondó eredmény azt fejezi ki, hogy ekkor a beírt

A B C

háromszögben

C

-nél derékszög van, és a háromszög magasságpontja azonos

C

-vel.

Major Zoltán (Budapest, Apáczai Csere J. Gyak. Gimn., IV. o. t.)

II. megoldás. Vegyük alapul az

\begin{matrix} \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 \end{matrix}

egyenletű ellipszist, a beírt

A B C

háromszög

A

csúcsának a

(- a,0)

B

-nek az

(a,0)

C

-nek az

(u, v)

pontot, az utóbbira tehát teljesül

\begin{matrix} \frac{u^{2}}{a^{2}} + \frac{v^{2}}{b^{2}} = 1, és | u | \neq a . \end{matrix}

(1)

Ekkor az

M

magasságpont abszcisszája a

C

-ből induló magasságvonal révén

u

. Az

A C

egyenes iránytangense

v / (v + a)

, így a

B

-ből induló magasságvonal egyenlete

\begin{matrix} y = - \frac{u + a}{v} (x - a), \end{matrix}

tehát

M

ordinátája.

x = u

helyettesítéssel, majd

(1)

alapján

u

-t kiküszöbölve

\begin{matrix} y_{M} = - \frac{u^{2} - a^{2}}{v} = \frac{1}{v} (a^{2} - u^{2}) = \frac{a^{2}}{b^{2}} v . \end{matrix}

(2)

Ebből ugyanúgy olvashatjuk ki

M

mértani helyének leírását, mint az I. megoldásban. Vagy pedig,

(2)

-ből

(1)

alapján

v

-t kiküszöbölve és

u = x_{M}

átírással a mértani hely egyenlete

\begin{matrix} y_{M} = \frac{a}{b} \sqrt[]{a^{2} - x_{M}^{2}}, \\ \frac{x_{M}^{2}}{a^{2}} + \frac{y_{M}^{2}}{{(a^{2} / b)}^{2}} = 1, és | x_{M} | \neq a . \end{matrix}

Mármost, a szokásos

a > b

nagyságviszonyt tekintve, az az eset áll előttünk, amikor a beírt háromszög rögzített oldala az ellipszis nagytengelye. A számításban azonban ezt nem használtuk fel, az

a

b > a

esetére is érvényes, így egy csapásra azt az esetet is elintéztük, amelyben a kistengelyt rögzítjük a háromszög oldalának.

Szabó Kálmán (Miskolc, Földes F. Gimn., IV. o. t.)

Megjegyzés. Ajánljuk az érdeklődőknek a feladat módosításának a megvizsgálását arra az esetre, ha a beírt háromszög egyik oldala az adott ellipszisnek tetszőleges, rögzített átmérője.