Kezdőlap


Feladat:	712. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Ádám Antal , Kaiser Marianna
Füzet:	1956/május, 137 - 140. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Feladat
Hivatkozás(ok):	Feladatok: 1955/november: 712. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Ismeretes, hogy a háromszög súlyvonalai az oldalakkal a következőképpen fejezhetők ki (II. oszt. gimn. tankönyvön kívül lásd K. M. L. VII. kötet, 3‐4. szám. 1953. nov. 510. feladat 88‐89. oldal):

\begin{matrix} s_{a} = \frac{1}{2} \sqrt[]{2 b^{2} + 2 c^{2} - a^{2}}, & (3) \\ s_{b} = \frac{1}{2} \sqrt[]{2 a^{2} + 2 c^{2} - b^{2}}, \\ s_{c} = \frac{1}{2} \sqrt[]{2 a^{2} + 2 b^{2} - c^{2}} . \end{matrix}

A cosinus-tétel alapján

\begin{matrix} cos α = \frac{b^{2} + c^{2} - a^{2}}{2 b c}, \end{matrix}

és így

\begin{matrix} cotg α = \frac{cos α}{sin α} = \frac{b^{2} + c^{2} - a^{2}}{2 b c sin α} = \frac{b^{2} + c^{2} - a^{2}}{4 t}, \end{matrix}

(4)

ahol

t

a háromszög területe (1. ábra).

1. ábra

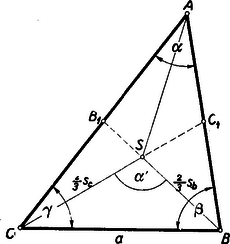A (4) összefüggést a

B C S_{▵}

-ben

α'

-re alkalmazva, (3) figyelembevételével

\begin{matrix} cotg α' = \frac{{(\frac{2}{3} s_{b})}^{2} + {(\frac{2}{3} s_{c})}^{2} - a^{2}}{4 \cdot \frac{t}{3}} = \frac{4 s_{b}^{2} + 4 s_{c}^{2} - 9 a^{2}}{12 t} = & (5) \\ = \frac{(2 a^{2} + 2 c^{2} - b^{2}) + (2 a^{2} + 2 b^{2} - c^{2}) - 9 a^{2}}{12 t} = \frac{b^{2} + c^{2} - 5 a^{2}}{12 t} . \end{matrix}

Másrészt (4) alapján

\begin{matrix} 2 cotg β + 2 cotg γ = \frac{a^{2} + c^{2} - b^{2}}{2 t} + \frac{a^{2} + b^{2} - c^{2}}{2 t} = \frac{a^{2}}{t}, \end{matrix}

és így (5) felhasználásával

\begin{matrix} cotg α - (2 cotg β + 2 cotg γ) = \frac{b^{2} + c^{2} - a^{2}}{4 t} - \frac{4 a^{2}}{4 t} = \\ = \frac{b^{2} + c^{2} - 5 a^{2}}{4 t} = 3 cotg α' . \end{matrix}

Ezzel az (1) összefüggést bebizonyítottuk.
(5) alapján

\begin{matrix} cotg α' + cotg β' + cotg γ' = \frac{b^{2} + c^{2} - 5 a^{2} + a^{2} + c^{2} - 5 b^{2} + a^{2} + b^{2} - 5 c^{2}}{12 t} = & (6) \\ = \frac{- 3 a^{2} - 3 b^{2} - 3 c^{2}}{12 t} = - \frac{a^{2} + b^{2} + c^{2}}{4 t} . \end{matrix}

(4) alapján

\begin{matrix} cotg α + cotg β + cotg γ = \frac{b^{2} + c^{2} - a^{2} + a^{2} + c^{2} - b^{2} + a^{2} + b^{2} - c^{2}}{4 t} = & (7) \\ = \frac{a^{2} + b^{2} + c^{2}}{4 t} . \end{matrix}

(6) és (7) összevetéséből következik a bizonyítandó (2) összefüggés.

Ádám Antal (Bp., VIII., Széchenyi g. III. o. t.)

II. megoldás: A súlyvonalak és oldalak közötti összefüggés, valamint a cosinus-tétel felhasználása nélkül is bizonyítható tételünk.
Helyezzük el az

A B C

háromszöget egy derékszögű koordináta-rendszerben, amint azt a 2. ábra mutatja.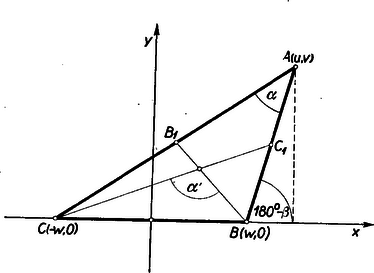

2. ábra

B A

egyenes irányhatározója

m_{1} = \frac{v}{u - w}

, a

C A

egyenesé

m_{2} = \frac{v}{u + w}

, tehát az általuk bezárt

α

szögre

\begin{matrix} cotg α = \frac{1 + m_{1} m_{2}}{m_{1} - m_{2}} = \frac{1 + \frac{v^{2}}{(v - w) (v + w)}}{\frac{v}{u - w} - \frac{v}{u + w}} = \frac{u^{2} - w^{2} + v^{2}}{v (u + w) - v (u - w)} = \frac{u^{2} + v^{2} - w^{2}}{2 v w} . \end{matrix}

Az ábráról közvetlenül leolvasható:

\begin{matrix} cotg β = - cotg (180^{\circ} - β) = - \frac{u - w}{v}, cotg γ = \frac{u + w}{v}, \end{matrix}

tehát

\begin{matrix} cotg α - 2 cotg β - 2 cotg γ = \frac{u^{2} + v^{2} + w^{2}}{2 v w} + \frac{2 u - 2 w}{v} - \frac{2 u + 2 w}{v} = & (8) \\ = \frac{u^{2} + v^{2} - w^{2} + 4 u w - 4 w^{2} - 4 u w - 4 w^{2}}{2 v w} = \frac{u^{2} + v^{2} - 9 w^{2}}{2 v w} . \end{matrix}

B_{1}

és

C_{1}

oldalfelezőpontok koordinátái:

(\frac{u - v}{2}, \frac{v}{2}), ill. (\frac{u + v}{2}, \frac{v}{2})

, és így a

B B_{1}

, ill.

C C_{1}

súlyvonalak iránytangensei

\begin{matrix} m_{1}' = \frac{\frac{v}{2}}{\frac{u - w}{2} - w} = \frac{v}{u - 3 w}, m_{2}' = \frac{\frac{v}{2}}{\frac{u + w}{2} + w} = \frac{v}{u + 3 w} . \end{matrix}

Tehát az általuk bezárt

α'

szögre

\begin{matrix} cotg a' = \frac{1 + m'_{1} m'_{2}}{m'_{1} - m'_{2}} = \frac{1 + \frac{v^{2}}{(u - 3 w) (u + 3 w)}}{\frac{v}{u - 3 w} - \frac{v}{u + 3 w}} = & (9) \\ = \frac{u^{2} - 9 w^{2} + v^{2}}{v (u + 3 w) - v (u - 3 w)} = \frac{u^{2} + v^{2} - 9 w^{2}}{6 v w} . \end{matrix}

(8) és (9) összevetése szolgáltatja (1)-et.
Ha az (1) összefüggést mindhárom szögre felírjuk:

\begin{matrix} 3 cotg α' = cotg α - 2 cotg β - 2 cotg γ, \\ 3 cotg β' = cotg β - 2 cotg α - 2 cotg γ, \\ 3 cotg γ' = cotg γ - 2 cotg α - 2 cotg β, \end{matrix}

e három egyenletet összeadjuk és mindkét oldalt hárommal osztjuk, nyerjük a bizonyítandó (2) összefüggést.

Kaiser Marianna (Bp., II., Hámán Kató lg. IV. o. t.)