| Feladat: | 690. matematika feladat | Korcsoport: 14-15 | Nehézségi fok: átlagos |
| Megoldó(k): | Bánhidy K. , Bártfai P. , Bayer J. , Belinczky G. , Csiszár Imre , Gerentsér Irma , Heinemann Z. , Jakubovics J. , Jedlovszky Pál , Kálmán Gy. , Kim Kvang Jan , Krem A. , Legéndy K. , Makkai M. , Morelli Klára , PasitkaB. , Quittner P. , Rázga T. , Szántó A. , Szeidl B. , Vásárhelyi B. , Vigassy Gy. , Zsombok Z. | ||
| Füzet: | 1956/február, 44 - 46. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Szabályos testek, Térelemek és részeik, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1955/május: 690. matematika feladat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. a) Először vizsgáljuk meg, hogy a gúla csúcsán átmenő 4 sík hány részre osztja a teret. A 650. feladat megoldásánál (K. M. L. X. kötet, 5. sz.) megmutattuk, hogy három sík, amely egy pontban metszi egymást, a teret nyolc részre bontja, míg egy negyedik sík, mely az előbbiekhez képest általános helyzetű ‐ tehát a három sík közös pontján nem megy át és sem valamelyik előző síkkal, sem két előző sík metszésvonalával nem párhuzamos ‐ 7 térrészt vág ketté, úgyhogy összesen 15 térrész keletkezik, melyek közül egy térrész véges, a többi végtelen. Ha a negyedik sík a három sík közös pontján megy át, a 15 térrész közül a véges térrész ponttá fajul, azaz 14 térrész jön létre. (Képzeljünk pl. a 151. oldalon az ábrán az sík helyett a ponton átmenő -vel párhuzamos síkot.) 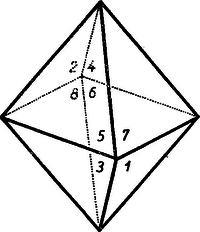 Az első síkpár a teret három részre bontja; az első és második síkpár együtt kilenc részre; az első, második és harmadik együtt 27-re. (E három síkpár egy véges térrészt: paralelepipidont határol. Eddig a feladat lényegében egyezik a 650. feladat első részével.) Tekintsük a negyedik síkpár egyik síkját, a 7 jelzésű vonalkázott háromszög síkját (2. ábra). 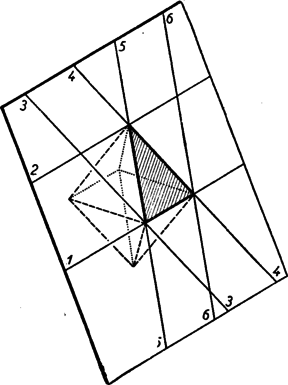 Ezt az előző hat sík három párhuzamos egyenesben metszi, az ábrán látható módon, pl. az 1 jelzésű egyenes az 1 jelzésű sík metszésvonala a 7. jelzésű vonalkázott síkkal, s i. t. A keletkezett metszésvonalak ‐ amint az ábráról leolvasható ‐ a síkot 16 részre bontják, tehát ez a sík 16 térrészt vág ketté, éppígy a vele párhuzamos 8 jelzésű sík is. Összesen tehát térrész keletkezik.
II. megoldás. Ugyanezt az eljárást követjük, mint az idézett 650. feladat II. megoldásánál. a) A négyzetes gúlából, lapon, élen és csúcson kilépve új térrészbe jutunk. Észre kell azonban vennünk hogy ezek a térrészek az eredeti gúlával együtt még nem töltik ki teljesen a teret, 4 térrész kimarad. Ezekbe közvetlenül eljuthatunk a gúla csúcsánál keletkező négyoldalú testszöglet csúcsszögletétől a csúcsszöglet lapjain keresztül. (A térrészek elképzelésénél ne hagyjuk számításon kívül két‐két szemközti oldallap síkjának metszésvonalát, melyek a csúcson mennek át és párhuzamosak egy‐egy alapéllel.) Összesen tehát térrész keletkezik. b) Az oktaéderlapok kiterjesztésével minden lapra egy‐egy tetraéder épül rá. Így a térrészek összeszámolásánál figyelembe kell vennünk a tetraéderekből való kilépéssel keletkező új térrészeket is. Az oktaéderből lapon, élen és csúcson kilépve új térrészbe jutunk. A tetraéderek lapjain kilépve nem jutunk új térrészbe. (Vagy az oktaéderbe jutunk vissza vagy olyan térrészbe kerülünk, amelybe kiléphetünk az oktaéder élén keresztül.) A tetraéder alapélein keresztül (a tetraéder és oktaéder közös élein) szintén nem jutunk új térrészbe, hanem egy lapra épített tetraéderbe. A tetraéder oldalélein keresztül oly térrészekbe jutunk, melyekbe egy másik tetraéder alaplapjának csúcsán át is eljuthatunk. Így végül is minden tetraédernél azt a négy‐négy térrészt kell számításba vennünk, amelyekbe a csúcsokon keresztül jutunk ki. Az összes térrészek száma: , melyek az egész teret kitöltik.
|