Feladat: 686. matematika feladat Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Almási Lajos ,  Bánhidy Kálmán ,  Bártfai P. ,  Bayer J. ,  Benkő J. ,  Bognár P. ,  Csák J. ,  Csiszár Imre ,  Daróczy Z. ,  Deres J. ,  Forgó G. ,  Forgó I. ,  Frivaldszky S. ,  Füst Gy. ,  Gerencsér I. ,  Gulácsy Sára ,  Heinemann Z. ,  Hidas P. ,  Huszár M. ,  Jakubovics J. ,  Jedlovszky P. ,  Kálmán Gy. ,  Katona P. ,  Kereszti I. ,  Kiss P. ,  Krakóczki F. ,  Krem A. ,  Kuti J. ,  Legéndy K. ,  Lindner I. ,  Makkai M. ,  Orlik P. ,  Papp K. ,  Pasitka B. ,  Perneczky L. ,  Rázga T. ,  Rédl Gy. ,  Soós T. ,  Stahl J. ,  Surán G. ,  Szabados J. ,  Szántó A. ,  Szeidl B. ,  Szentai E. ,  Trembiczki I. ,  Ványai L. ,  Vásárhelyi B. ,  Vértes P. ,  Vigassy Gy. ,  Zsombok Z. 
Füzet: 1956/január, 16 - 18. oldal  PDF  |  MathML 
Témakör(ök): Mértani helyek, Parabola, mint kúpszelet, Feladat
Hivatkozás(ok):Feladatok: 1955/május: 686. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Legyen a parabola egyenlete y2=4tx, vagyis a fókusznak az origótól való távolsága OF=t. Messe a parabola érintője a csúcsérintőt, azaz az y tengelyt, egy E pontban és legyen OE=u (1. ábra), akkor az EF egyenes iránytényezője -ut, és így az EF-re merőleges érintő egyenlete

y=tux+u.(1)
 
1. ábra
 

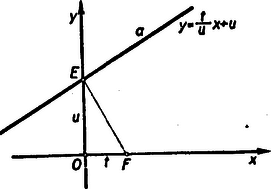A másik két érintő által az y tengelyből lemetszett részeket v, ill. w-vel jelölve, e két érintő egyenlete
y=tvx+v,(2)
és
y=twx+w.(3)

Az érintők alkotta háromszög egyik csúcsának koordinátáit megkapjuk, ha megoldjuk pl. az (1) és (2) egyenletrendszert. Elvégezve a számítást nyerjük, hogy
x=uvt,y=u+v.

E csúcsból kiinduló magasság merőleges a (3) egyenesre; egyenlete tehát
y-(u+v)=-wt(x-uvt).(4)

Hasonlóképpen az (1) egyenesre merőleges magasságvonal egyenlete
y-(v+w)=-ut(x-vwt).(5)
(4) és (5)-ből a magasságpont koordinátái
x=-t,(6)y=u+v+w+uvwt2.(7)



(6) azt mutatja, hogy a magasságpontok a direktrikszen vannak, (7)-ből pedig következik, hogy minden megadott t és y esetén ‐ tehát a direktriksz bármely pontjához ‐ meg lehet választani az u, v és w értékeket úgy, hogy (7) teljesüljön. A keresett mértani hely tehát a direktriksz.
 

Almási Lajos (Bp. II., Rákóczi g. IV. o. t.)
 

II. megoldás: Jelöljük a parabola fókuszát F-fel, csúcsérintőjét e-vel, a három adott érintőt a-val, b-vel és c-vel. Az adott érintők messék a csúcsérintőt rendre az E, G és H pontban, egyébként a betűzést a 2. ábra mutatja.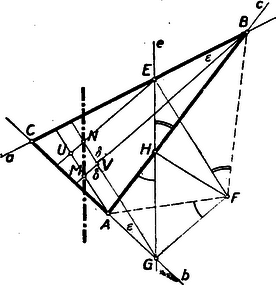
 
 
2. ábra
 

Először két tetszőleges adott érintőhöz, pl. a és b-hez vegyük hozzá harmadiknak a csúcsérintőt. Az így keletkező ECG▵ magassági pontja legyen N. A szerkesztés szerint EFGN paralelogramma, tehát az N pont a direktrikszen van. Tekintsük azután az ABC▵-et. Az ECG▵ és ABC▵ két-két magasság-vonala szintén paralelogrammát határoz meg. Ha sikerülne kimutatni, hogy ez az NVMU paralelogramma az EFGN paralelogrammához hasonló, ebből máris következnék ‐ tekintve, hogy a paralelogrammák hasonló helyzetűek ‐, hogy az M pont is a direktrikszen van. Elég volna kimutatni, hogy
NV:MV=EF:GF.(1)

Tekintsük a VBEN és VGAM trapézeket, melyekben az alapon fekvő szögek egyenlők (a V-nél fekvő δ szögek csúcsszögek, a B, ill. G-nél fekvő ε szögek merőleges szárú szögek). Ezért a nem párhuzamos oldalak aránya egyenlő, vagyis
NV:MV=EB:AG.(2)

Másrészt
FEB▵∼FGA▵.
Ugyanis az F-nél fekvő egyíves szög egyenlő a H-nál fekvő egyíves szöggel, mert AGFH húrnégyszög. Hasonló okból a kétíves szögek is egyenlők, továbbá a H-nál fekvő egyíves és kétíves szög csúcsszögek. Ezenkívül FEB▵ és FCA▵ derékszögűek. A háromszögek hasonlóságából következik, hogy
EB:AG=EF:GF,(3)
amivel ‐ figyelemmel (2)-re ‐ az (1) alatti állításunkat bebizonyítottuk.
 

Csiszár Imre (Bp. I., Petőfi g. III. o. t.)
 

III. megoldás: Ismeretes, hogy az érintőnek a csúcsérintővel alkotott metszéspontjában az érintőre állított merőleges átmegy a parabola fókuszán. Ennélfogva az ABC érintőháromszögnek az e csúcsérintő Simson-egyenese, vagyis F rajta van az a, b és c érintők alkotta ABC▵ köré írt körön.
Ugyancsak ismeretes, hogy valamely P ponthoz tartozó Simson-egyenes felezi a PM távolságot, ahol M a háromszög magassági pontja (ld. 659. feladatot, XI. kötet 3‐4. sz. 1955. nov. 89‐90. old.).
Mivel minden érintőháromszög köré írt kör átmegy az F fókuszon, és utóbbihoz tartozó Simson-féle egyenes mindenkor a csúcsérintő, azért az érintőháromszögek magasságpontjainak mértani helyét a csúcsérintőnek F-ből, mint hasonlósági középpontból kétszeres távolságra való kivetítése adja, ami viszont nem más, mint a parabola vezéregyenese.
 

Bánhidy Kálmán (Debrecen, Ref. g. III. o. t.)