Kezdőlap


Feladat:	683. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Kauker János , Pruzsina János
Füzet:	1956/január, 11 - 12. oldal		PDF \| MathML
Témakör(ök):	Parabola egyenlete, Mértani helyek, Feladat
Hivatkozás(ok):	Feladatok: 1955/április: 683. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Legyen a parabola egyenlete $y = 2 p x$ . Felhasználjuk a parabola érintőjének azt a tulajdonságát, hogy az $x$ tengelyből negatív irányban akkora szakaszt vág le, mint az érintési pont abszcisszája, az $y$ tengelyből pedig akkorát, mint az érintési pont ordinátájának fele.
Tehát a keresett mértani hely pontjainak koordinátái

\begin{matrix} x = - x_{1}, y = \frac{y_{1}}{2}, \end{matrix}

amiből

\begin{matrix} x_{1} = - x, y_{1} = 2 y . \end{matrix}

x_{1}

és

y_{1}

kielégíti a parabola egyenletét, tehát

\begin{matrix} {(2 y)}^{2} = 2 p (- x), \end{matrix}

vagyis

\begin{matrix} y^{2} = - \frac{p}{2} x . \end{matrix}

Ez egy parabola egyenlete, melynek csúcsa az origó, tengelye az

x

tengely negatív fele, paramétere az adott parabola paraméterének negyedrésze (1. ábra).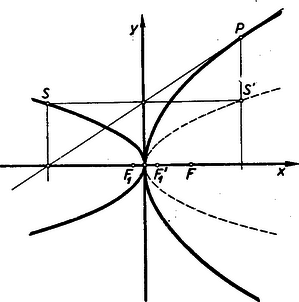

1. ábra

Könnyű belátni, hogy e parabola minden pontjának (kivéve az origót) adjungáltja az eredeti parabola egy érintője.

Kauker János (Veszprém, Lovassy L. g. IV. o. t.)

Megjegyzés: A kiindulási állítás szerint az érintőhöz adjungált pont abszcisszája egyenlő az érintési pont abszcisszájával és vele ellenkező előjelű, az adjungált pont ordinátája pedig az érintési pont ordinátájának a fele. Eszerint az adjungált pontot úgy szerkeszthetjük, hogy az érintési pontnak a parabola tengelyétől mért távolságát felére csökkentjük, majd az így nyert pontot az

y

tengelyre nézve tükrözzük. Ámde a 618. feladatnál (ld. X. kötet 1. szám, 1955 január, 25‐27. old.) bebizonyítottuk, hogy a felezőpontok mértani helye parabola, úgyhogy az adjungált pontok mértani helye ennek a parabolának a tükörképe.

II. megoldás: Felhasználjuk a parabola érintőjének azt a tulajdonságát, hogy a csúcsérintővel való metszéspontján áthaladó, az érintőre merőleges egyenes átmegy a fókuszon.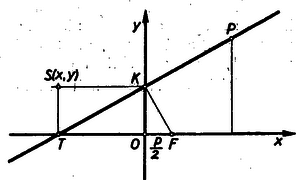

2. ábra

Eszerint (2. ábra) a

T K F ▵

derékszögű,

O F = \frac{p}{2}

O K = | y |

O T = | x |

, ahol

x, y

S

pont koordinátái, és így a derékszögű háromszög magasságának mértani közép tulajdonsága szerint

y^{2} = \frac{p}{2} | x |

, de nyilvánvaló, hogy az

S

pontok abszcisszái negatívok, tehát a keresett pontok rajta vannak az

\begin{matrix} y^{2} = - \frac{p}{2} x \end{matrix}

parabolán. Könnyű belátni, hogy a

(0, 0)

pont kivételével e parabola minden pontja megfelel a feladatnak.

Pruzsina János (Pécs, Bányaip. t. III. o. t.)