Kezdőlap


Feladat:	202. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1954/december, 142 - 144. oldal		PDF \| MathML
Témakör(ök):	Háromszögek szerkesztése, Gyakorlat
Hivatkozás(ok):	Feladatok: 1954/április: 202. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Képzeljük a feladatot megoldottnak. A $C_{1}$ , pont lehet az $A B$ szakaszon (l. típus), vagy pedig az $A B$ oldal meghosszabbításán (2. típus ‐ az 1. ábrán *-gal jelölve).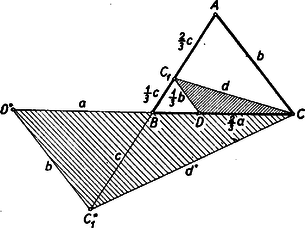

1. ábra

C_{1}

, (ill.

C_{1}^{*}

) ponton át a

b

oldallal húzott párhuzamos messe a

B C = a

oldalt, a

D

(ill.

D^{*}

) pontban. A feladat értelmében a keletkezett

C_{1} D C ▵

oldalai:

C_{1} D = \frac{1}{3} b

D C = \frac{2}{3} a

C C_{1} = d

míg a keletkezett

C_{1}^{*} D^{*} C ▵

oldalai:

C_{1}^{*} D^{*} = b

D^{*} C = 2 a

, és

C C_{1}^{*} = d

. Mindkét háromszögnek mindhárom oldala adott, tehát megszerkeszthető. E háromszögek birtokában a keresett

A B C ▵

megszerkesztése már nem probléma.
Az 1. típus esetén a megoldhatóság szükséges és elégséges feltétele, hogy

d < \frac{2}{3} a + \frac{1}{3} b = \frac{2 a + b}{3}

. A 2. típusnál a megoldhatóság szükséges és elégséges feltétele, hogy

b + d > 2 a

, vagyis

d > | 2 a - b |

.
Mindkét típusú megoldás csak akkor lehetséges, ha

\begin{matrix} | 2 a - b | < d < \frac{2 a + b}{3} . \end{matrix}

(1)

Vizsgáljuk meg, hogy milyen feltételeket kell

a

és

b

-nek kielégítenie, hogy (1) teljesülhessen.
Három esetet kell megkülönböztetni:

\begin{matrix} 1. 0 < 2 a - b, 2. 0 < b - 2 a és 3. 0 = b - 2 a \end{matrix}

A (3) esetben (1) mindig teljesül. Az 1. esetben, azaz ha

\frac{b}{2} < a

\begin{matrix} 2 a - b < \frac{2 a + b}{3}, 6 a - 3 b < 2 a + b, 4 a < 4 b, \end{matrix}

azaz

\begin{matrix} \frac{b}{2} < a < b . \end{matrix}

A 2. esetben, vagyis ha a

a < \frac{b}{2}

\begin{matrix} b - 2 a < \frac{2 a + b}{3}, 3 b - 6 a < 2 a + b, 2 b < 8 a, \end{matrix}

azaz

\begin{matrix} \frac{b}{4} < a < \frac{b}{2} . \end{matrix}

Tehát

\begin{matrix} \frac{b}{4} < a < b \end{matrix}

(2)

esetén áll fenn (1)

és ha most

α

)

| 2 a - b | < d < \frac{2 a + b}{3}

, akkor feladatunknak

2

(egy 1. és egy 2. típusú) megoldása van (2. ábra).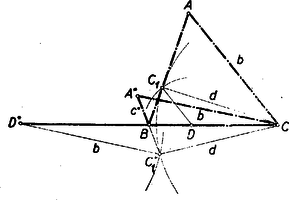

2. ábra

β

)

d < | 2 a - b |

, akkor csak egy

1. típusú megoldás van,

γ

)

\frac{2 a + b}{3} < d

, akkor csak egy

2. típusú megoldás van.
Ha

\begin{matrix} b < a, vagy 0 < a < \frac{b}{4} \end{matrix}

(3)

akkor

\begin{matrix} \frac{2 a + b}{3} < | 2 a - b | \end{matrix}

és ez esetben, ha

α

)

\frac{2 a + b}{3} < d < | 2 a - b |

, akkor egyáltalán nincs megoldás,

β

)

d < \frac{2 a + b}{3}

, akkor csak egy 1. típusú,

γ

)

| 2 a - b | < d

, akkor csak egy 2. típusú megoldás van.
Ha

\begin{matrix} a = b \end{matrix}

(4)

akkor

\frac{2 a + b}{3} = 2 a - b = a

és így ha

α

)

d < a = b

, akkor csak egy 1. típusú

β

)

a = b < d

, akkor csak egy 2. típusú megoldás van.

γ

)

a - b = d

-hez nem tartozik valódi háromszög.
Végül ha

\begin{matrix} a = \frac{b}{4}, \end{matrix}

(5)

akkor

\frac{2 a + b}{3} = b - 2 a = \frac{b}{2}

, és így, ha most

α

)

d < \frac{b}{2}

, akkor csak egy 1. típusú,

β

)

d > \frac{b}{2}

, akkor csak egy 2. típusú megoldás van.

γ

)

d = \frac{b}{2}

esetén a háromszög egyenesszakasszá fajul.

Megfelelő taglalást senki sem küldött be.