Kezdőlap


Feladat:	382. matematika feladat	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Kántor S. , Reichlin V. , Zatykó L.
Füzet:	1952/április, 66 - 67. oldal		PDF \| MathML
Témakör(ök):	Függvényvizsgálat, Bernoulli-féle egyenlőtlenség, Jensen-féle egyenlőtlenség, Feladat
Hivatkozás(ok):	Feladatok: 1951/december: 382. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A IV. közleményben említettünk a konvexségre jellemző néhány újabb geometriai tulajdonságot. Így egy $f (x)$ függvény görbéje konvex, egy szakaszon, ha e szakasz bármely három növekvő abszcisszák szerint következő $P_{1}$ , $P_{2}$ , $P_{3}$ pontjára fennáll, a következő tulajdonságok bármelyike:

a) hogy a

P_{1} P_{2}

húr a

P_{1} P_{3}

húr alatt van,
b) hogy a

P_{2} P_{3}

húr a

P_{1} P_{3}

húr alatt van,
c) hogy a

P_{1} P_{2}

húr meghosszabbítása a

P_{2} P_{3}

húr alá fut.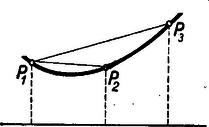

Fejezzük ki e tulajdonságokat az algebra nyelvén. Ha két egyenesnek egy pontja közös, akkor egy nagyobb abszcissza-értéknél az van magasabban, egy kisebb abszcissza-értéknél pedig az van mélyebben, amelyiknek a meredeksége nagyobb. Az

f (x)

görbe

ξ

és

ξ'

abszcisszájú pontok közti húrjának a meredeksége pedig

\begin{matrix} \frac{f (ξ') - f (ξ)}{ξ' - ξ} . \end{matrix}

Így ha a három pont abszcisszái

x_{1}

x_{2}

x_{3}

, akkor a fenti tulajdonságokat rendre az

\begin{matrix} \frac{f (x_{2}) - f (x_{1})}{x_{2} - x_{1}} < \frac{f (x_{3}) - f (x_{1})}{x_{3} - x_{1}}, & (a) \\ \frac{f (x_{3}) - f (x_{1})}{x_{3} - x_{1}} < \frac{f (x_{3}) - f (x_{2})}{x_{3} - x_{2}}, & (b) \\ \frac{f (x_{2}) - f (x_{1})}{x_{2} - x_{1}} < \frac{f (x_{3}) - f (x_{2})}{x_{3} - x_{2}} & (c) \end{matrix}

egyenlőtlenségek fejezik ki. Mindegyik egyenlőséget átszorozhatjuk a nevezők szorzatával, mert feltétel szerint

x_{1} < x_{2} < x_{3}

és így mindegyik nevező pozitív. Ha még a kapott egyenlőtlenséget nullára redukáljuk és

f (x_{1})

f (x_{2})

f (x_{3})

-at röviden

y_{1}

y_{2}

y_{3}

-mal jelöljük, akkor mindhárom egyenlőtlenségből az

\begin{matrix} x_{1} (y_{2} - y_{3}) + x_{2} (y_{3} - y_{1}) + x_{3} (y_{1} - y_{2}) > 0 \end{matrix}

(t)

egyenlőtlenséghez jutunk és ez vissza is alakítható a három egyenlőtlenség bármelyikévé. A (t) egyenlőtlenség baloldalán álló kifejezés a

P_{1} P_{2} P_{3}

háromszög kétszeres területének kifejezése koordináták segítségével. Így a kapott egyenlőtlenség szerint a három pont nem sorakozhat egy egyenesen, sőt azt is tudjuk, hogy ha a területet pozitív előjellel adja a képlet, akkor a

P_{1}

P_{2}

P_{3}

csúcsok az óra járásával ellenkező körüljárás sorrendjében következnek. Ez a geometriai tulajdonság tekinthető a konvexség újabb geometriai jellemzésének is, amiből könnyen következnek az (a), (b) és (c) tulajdonságok. Könnyű látni, hogy ez a geometriai tulajdonság tartalmazza a kéttagú súlyozott Jensen-egyenlőtlenséget is, amit eredetileg a konvexség jellemzésére használtunk. Utóbbit úgy kaptuk, hogy az algebra nyelvére fordítottuk a következő tulajdonságot: a

P_{2}

pont a

P_{1} P_{3}

húr alatt van. Mivel

x_{2}

(x_{1}, x_{3})

szakaszt

(x_{2} - x_{1}) : (x_{3} - x_{2})

arányban osztja, így a

P_{1} P_{3}

húr

x_{2}

abszcisszájú pontja ugyanilyen arányban osztja a húrt, tehát ordinátája

\begin{matrix} \frac{(x_{3} - x_{2}) f (x_{1}) + (x_{2} - x_{1}) f (x_{3})}{x_{3} - x_{1}} \end{matrix}

s így a mondott tulajdonságot az

\begin{matrix} f (x_{2}) < \frac{(x_{3} - x_{2}) f (x_{1}) + (x_{2} - x_{1}) f (x_{3})}{x_{3} - x_{1}} \end{matrix}

(j)

egyenlőtlenség fejezi ki.
Ha itt egyrészt

\frac{x_{3} - x_{2}}{x_{3} - x_{1}} = q_{1}

\frac{x_{2} - x_{1}}{x_{3} - x_{1}} = q_{2}

-t írunk, tehát

q_{1} + q_{2} = 1

és

x_{2}

helyébe a vele azonos

q_{1} x_{1} + q_{2} x_{3}

értéket,

(

ami azt fejezi ki, hogy

x_{2}

(x_{1}

x_{3})

szakaszt

q_{2} : q_{1} = (x_{2} - x_{1}) : (x_{3} - x_{2})

arányban osztja

)

, akkor megkapjuk a Jensen-egyenlőtlenséget. Másrészt viszont a (j) egyenlőtlenség is átalakítható a (t) egyenlőtlenséggé, csupa olyan lépésekben, melyek ellenkező irányban is elvégezhetők, vagyis a (t) egyenlőtlenség átalakítható a Jensen-egyenlőtlenséggé is és viszont. Ebből az is következik, hogy az (a), (b), (c) egyenlőtlenségek mindegyike (és a (t) is) következik a Jensen-egyenlőtlenségből és megfordítva utóbbi is ezek bármelyikéből.