Kezdőlap


Feladat:	131. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bakó László , Bártfai P. , Beke Éva és Mária , Beleznay F. , Biczó G. , Boros P. , Csiszár I. , Deseő Katalin , Edőcsény Z. , Forgó G. , Fuchs T. , Harza T. , Kálmán Gy. , Katona P. , Kirz J. , Krammer G. , Pintér Z. , Quittner L. , Rázga T. , Szerb M. , Tarlacz L. , Tolnai T. , Uray L. , Zsombok Z.
Füzet:	1953/december, 147 - 148. oldal		PDF \| MathML
Témakör(ök):	Klasszikus valószínűség, Szöveges feladatok, Gyakorlat
Hivatkozás(ok):	Feladatok: 1953/április: 131. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Természetesen úgy kell felfogni a $≫$ táblára dobást $≪$ , hogy a pénzdarab középpontja a táblára esett. (Annak feltevése, hogy a pénzdarab teljes kiterjedésében a tábla belsejébe esett, komplikálja a feladatot, mert ez esetben a tábla szélső mezői kivételes szerepet játszanak.) A pénzdarab középpontja tehát biztosan valamely négyzet belsejébe, vagy határvonalára esik. Csak ezt az egy négyzetet kell tehát vizsgálni.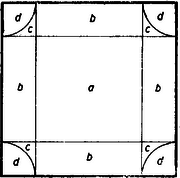
A középpontra nézve lehetséges eset a négyzet területének minden pontja. Mivel a négyzet oldala $\frac{40}{8} = 5 cm$ , azért a lehetséges terület $50^{2} = 2500 {m m}^{2}$ .
a) Ez esetben kedvező terület a pénzdarab középpontjára a négyzetnek mindazon pontja, amelynek távolsága a legközelebbi négyzetoldaltól $\geq$ a pénzdarab sugaránál, vagyis $9, 5 mm$ -nél. Ez a terület olyan négyzet, amelynek oldala $50 - 2 \cdot 9, 5 = 31 mm$ . (Az ábrán $a$ -val jelölve.) Tehát a keresett valószínűség

\begin{matrix} V_{a} = \frac{31^{2}}{50^{2}} = \frac{961}{2500} = 0, 3844. \end{matrix}

b) Ez esetben a pénzdarab középpontjára nézve kedvező (terület az ábránkon

b

-veI jelzett

4

téglalapból tevődik össze. Ezeknek összterülete ,

4 \cdot 31 \cdot 9, 5 = 1178 mm

és így

\begin{matrix} V_{b} = \frac{1178}{2500} = 0, 4712. \end{matrix}

c) A kedvező terület a középpontra nézve az ábrán

c

-veI jelzett

4

tartomány, amelyeknek összterületét megkapjuk, ha egy

19 mm

-es oldalhosszúságú négyzet területéből kivonjuk a beírt kör területét, vagyis

19^{2} - {9, 5}^{2} π = 77, 6 {m m}^{2}

, és így

\begin{matrix} V_{c} \approx \frac{77, 6}{2500} \approx 0, 0310. \end{matrix}

d) A kedvező terület ez esetben a

d

-vel jelzett négy negyedkör, amelyeknek összterülete

{9, 5}^{2} π \approx 283, 4 mm

, tehát

\begin{matrix} V_{d} \approx \frac{283, 4}{2500} \approx 0, 1134. \end{matrix}

Bakó László (Debrecen, Ref. g. II. o. t.)