Kezdőlap


Feladat:	111. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bakó L. , Beke Gy. , Beliczky Géza , Biczó Géza , Fodor Ilona , Papp Judit , Pátkai György , Quittner P. , Tolnai T.
Füzet:	1953/november, 115 - 117. oldal		PDF \| MathML
Témakör(ök):	Paralelogrammák, Pitagorasz-tétel alkalmazásai, Pont körüli forgatás, Hasonlósági transzformációk, Gyakorlat
Hivatkozás(ok):	Feladatok: 1953/február: 111. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: A betűzést az 1. ábra mutatja.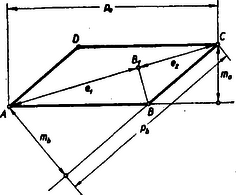

1. ábra

Pythagoras tételét írjuk fel rendre a következő négy derékszögű háromszögre :

A C C_{1} ▵

A C A_{1} ▵

C B C_{1} ▵

és

A B A_{1} ▵

\begin{matrix} e^{2} & = p_{a}^{2} + m_{a}^{2}, & (1) \\ e^{2} & = p_{b}^{2} + m_{b}^{2}, & (2) \\ m_{a}^{2} & = b^{2} - {(p_{a} - a)}^{2}, & (3) \\ m_{b}^{2} & = a^{2} - {(p_{b} - b)}^{2} . & (4) \end{matrix}

(1) és (2) összegébe behelyettesítve (3), ill. (4)-ből

m_{a}^{2}

ill.

m_{b}^{2}

értékét

\begin{matrix} 2 e^{2} = p_{a}^{2} + p_{b}^{2} + b^{2} - {(p_{a} - a)}^{2} + a^{2} - {(p_{b} - b)}^{2} = 2 a p_{a} + 2 b p_{b}, \end{matrix}

vagyis

\begin{matrix} e^{2} = a p_{a} + b p_{b} . \end{matrix}

Beliczky Géza (Czelldömölk, Gábor Áron g. II. o. t.)

II. megoldás: Bocsássuk a

B

csúcspontból (1. ábra) a

B B_{1}

merőlegest az

e

átlóra.

A B_{1} = e_{1}

B_{1} C = e_{2}

A B B_{1} ▵ \sim A C C_{1} ▵

, mert mindkettő derékszögű és egy hegyes szögük közös. Tehát

\begin{matrix} e_{1} : a = p_{a} : e, vagyis a p_{a} = e_{1} e . \end{matrix}

(1)

Hasonlóképpen

C B B_{1} ▵ \sim C A A_{1} ▵

, és így

\begin{matrix} e_{2} : b = p_{b} : e, vagyis b p_{b} = e_{2} e . \end{matrix}

(2)

(1) és (2) összege

\begin{matrix} a p_{a} + b p_{b} = e_{1} e + e_{2} e = e (e_{1} + e_{2}) = e^{2} . \end{matrix}

Pátkai György (Bp., IX., Fáy András g. II. o. t.)

Ez a megoldás lényegében megegyezik azzal, amikor az aránypárok helyett a

B A C ∢

és

B C A ∢

cosinusával dolgozunk.

III. megoldás: Tételünket területátalakítással is bizonyíthatjuk. A

C

pont merőleges vetülete az

A B

és

A D

oldalakra legyen

E

ill.

F

(2. áb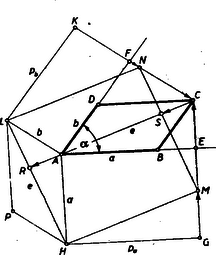ra).

2. ábra

Szerkesszünk

A E = p_{a}

fölé,

A E G H

téglalapot úgy, hogy

A H = a

, vagyis a téglalap területe

a p_{a}

. Hasonlóképpen

A F K L

területe

b p_{b}

.
Húzzuk meg a

H

-ból ill.

L

-ből az

L P | | A H

és

H P | | A L

egyeneseket. Ha a keletkező

A L P H

paralelogrammát

A

körül az óramutató járásával egyirányban

90

fokkal elforgatjuk, akkor

A L

átmegy

A D

-be és

A H

pedig

A B

meghosszabbításába. Így

H A L P ≃ A B C D

és előbbi

90

fokkal van elforgatva utóbbihoz képest, amiből következik, hogy

H L = A C = e

és

H L ⊥ A C

.
Ha az

A H G E

téglalap

G E

oldalát saját meghosszabbításában eltoljuk, amíg az

E

pont

C

-be és a

G

pont

M

-be kerül, akkor a nyert

A H M C

paralelogramma területe nyilván egyenlő a téglalap területével, amely

a p_{a}

.
Ugyanígy eltoljuk a

K F

szakaszt saját meghosszabbításában

N C

-be, akkor nyilván az

A L N C

paralelogramma területe is

b p_{b}

mint az

A L K F

téglalapé.
Ha most a két paralelogramma közös

A C

oldalát toljuk el saját meghosszabbításában, amíg az

A

pont

R

-be és a

C

pont

S

-be ér, akkor a két paralelogramma átalakult a velük egyenlő területű

H L N M

négyzetté, amelynek területe

e^{2}

. Tehát tényleg

\begin{matrix} a p_{a} + b p_{b} = e^{2} . \end{matrix}

Biczó Géza (Bp., II., Rákóczi g. II. o. t.)