Kezdőlap


Feladat:	110. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Székely Tamás , Zsombok Zoltán
Füzet:	1953/november, 114 - 115. oldal		PDF \| MathML
Témakör(ök):	Háromszögek geometriája, Körülírt kör, Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1953/február: 110. matematika gyakorlat

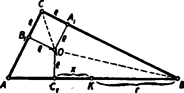
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: A körülírt kör középpontja $K$ az $A B$ átfogó felezőpontja, vagyis $A K = K B = r = 41$ (l. ábrát).

A beírt kör középpontját

O

-val és az

a

b

c

oldalakon lévő érintési pontokat rendre

A_{1}

B_{1}

C_{1}

-gyel jelölve,

O A_{1} C B_{1}

négyzet, melynek oldala

ϱ = 8

.
Ha a

C_{1} K

szakaszt

x

-szel jelöljük, akkor

\begin{matrix} a & = B A_{1} + A_{1} C = B C_{1} + A_{1} C = (r + x) + ϱ = r + ϱ + x, \\ b & = A B_{1} + B_{1} C = A C_{1} + B_{1} C = (r - x) + ϱ = r + ϱ - x, \\ c & = 2 r . \end{matrix}

Pythagoras tétele alapján,

r

és

ϱ

értékeit behelyettesítve

\begin{matrix} {(49 + x)}^{2} + {(49 - x)}^{2} = 82^{2}, \end{matrix}

azaz

\begin{matrix} x^{2} = 961, \end{matrix}

amiből

\begin{matrix} x_{1} = 31, x_{2} = - 31. \end{matrix}

Tehát

\begin{matrix} a = 49 \pm 31 = 80 ill. 18, b = 49 \mp 31 = 18 ill. 80, \end{matrix}

vagyis a befogók keresett mértékszáma

81 cm

és

18 cm

, az átfogó pedig

2 r = 82 cm

Zsombok Zoltán (Bp., IV., Könyves Kálmán g. I. o. t.)

II. megoldás: Ha a háromszög kerületét

2 s

-sel jelöljük, akkor a félkerület

\begin{matrix} s = A C_{1} + B A_{1} + C B_{1} = A C_{1} + B C + C B_{1} = 2 r + ϱ = 82 + 8 = 90, \end{matrix}

tehát

2 s = 180

. és így

\begin{matrix} a + b = 2 s - c = 180 - 82 = 98. \end{matrix}

(1)

Másrészt a háromszög területe

t = \frac{a b}{2} = s ϱ = 90 \cdot 8 = 720

, és így

\begin{matrix} 8 t = 4 a b = 5760 \end{matrix}

(2)

(1) négyzetéből kivonva (2)-t, nyerjük, hogy

\begin{matrix} {(a - b)}^{2} = 98^{2} - 5760 = 3844 = 62^{2} \end{matrix}

Nem megy az általánosság rovására, ha

a

-val jelöljük a nagyobbik befogót. Ez esetben tehát

\begin{matrix} a - b = 62 \end{matrix}

(3)

(1) és (3)-ból

\begin{matrix} a = 80 és b = 18 \end{matrix}

Székely Tamás (Bp., XVI., Corvin Mátyás g. II. o. t.)