Kezdőlap


Feladat:	101. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Almási L. , Bacsó N. , Bakó L. , Balogh J. , Bártfai P. , Bauer P. , Beke Éva és Mária , Beleznay Ferenc , Beliczky G. , Biczó G. , Biszterszky Sára , Boros P. , Csiszár I. , Csizmadia G. , Czili Gy. , Darázsi J. , Frivaldszky J. , Georgi F. , Gulácsy Sára , Gutai L. , Gyöngyös Gy. , Harza T. , Juhász Anna , Kálmán Gy. , Kása I. , Kovács Klára , Kulcsár Zsuzsa , Lackner Györgyi , Makai I. , Murray Erzsébet , Pátkai Gy. , Pázmándy Gy. , Pintér L. , Quittner P. , Roboz Ágnes , Szalay Éva , Szám F. , Szendrei I. , Szentai E. , Szerb Márta , Takács J. , Tolnai T. , Tóth I. , Uray L. , Várnai I. , Vértes P. , Zsombok Z.
Füzet:	1953/október, 51 - 52. oldal		PDF \| MathML
Témakör(ök):	Körök, Síkgeometriai szerkesztések, Terület, felszín, Gyakorlat
Hivatkozás(ok):	Feladatok: 1953/január: 101. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Jelöljük az adott körök sugarait $r_{1}$ , $r_{2}$ és $r_{3}$ -mal, a keresett körgyűrű külső és belső körének sugarát $R$ ill. $r$ -rel.
A feladat szerint

\begin{matrix} (R^{2} - r^{2}) π = (r_{1}^{2} + r_{2}^{2} + r_{3}^{2}) π, \end{matrix}

vagyis

\begin{matrix} \sqrt[]{R^{2} - r^{2}} = \sqrt[]{r_{1}^{2} + r_{2}^{2} + r_{3}^{2}} = a . \end{matrix}

a

távolság, a Pythagoras-tétel kétszer egymásutáni alkalmazásával, egyszerűen megszerkeszthető (1. ábra). Az

a

geometriai jelentése: egyrészt azon kör sugara, amelynek területe egyenlő az adott 3 kör területének összegével, másrészt, Pythagoras tétele alapján, nem egyéb, mint a keresett körgyűrű külső körében azon húr fele, amely érinti a belső kört (2. ábra).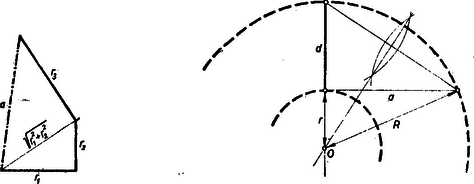

1. ábra 2. ábra

Eszerint derékszögű háromszöget szerkesztünk, amelynek egyik befogója a megszerkesztett

a

távolság és másik befogója a körgyűrű adott szélessége

d

. A keresett körgyűrű külső köre átmegy e derékszögű háromszög átfogójának végpontjain és az

O

középpontja a

d

befogót hordozó egyenesen van. A koncentrikus belső kör sugara

r = R - d

. E belső kör tehát érinti az

a

befogót a derékszög csúcspontjában.
A megoldhatóság feltétele, hogy

O

d

meghosszabbításán legyen, vagyis, hogy

a > d

, azaz

\sqrt[]{r_{1}^{2} + r_{2}^{2} + r_{3}^{2}} > d

. Ha

a = d

, akkor a belső kör ponttá és a körgyűrű

a

sugarú körré fajul.

Roboz Ágnes (Bp. VI., Varga Katalin lg. II. o. t.)

II. Megoldás:

a

-ból és

d

-ből (

d < a

) a keresett

R

és

r

távolságok a következőképpen is szerkeszthetők: Az

a = A B

távolság mindkét végpontjában, ugyanabban az irányban, merőleges félegyeneseket emelünk. A

B

-ben emelt merőlegesre felmérjük a

B C = d

távolságot (3. ábra).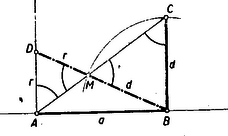

3. ábra

B C = d

sugárral

B

körül rajzolt kör messe az

A D

átfogót

M

-ben. A

B M

egyenes és az

A

-ban

A B

-re emelt merőleges metszéspontja legyen

D

. Akkor nyilván az ábrában ívekkel jelölt szögek egyenlők és így

D A = D M

.
Mivel

a^{2} = R^{2} - r^{2} = {(r + d)}^{2} - r^{2}

, ezért

D A = D M = r

és

D B = r + d = R

Beleznay Ferenc (Bp. V., Piarista g. II. o. t.)

III. megoldás:

a^{2} = R^{2} - r^{2} = (R + r) (R - r) = 2 \cdot \frac{R + r}{2} d

\frac{R + r}{2}

geometriai értelme: a >>középkör<< sugara. Utóbbit

ϱ

-val jelölve

\begin{matrix} a^{2} = 2 d ϱ, \end{matrix}

amiből,

a

és

d

ismeretében,

ϱ

(a tankönyvben tárgyalt) többféle módon megszerkeszthető.

ϱ + \frac{d}{2} = R

és

ϱ - \frac{d}{2} = r