Kezdőlap


Feladat:	267. matematika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Béres A. , Dávid P. , Durst E. , Kántor S. , Lipák J. , Osztein P. , Sajó I. , Seitz K. , Villányi O. , Viski Mária
Füzet:	1951/augusztus, 90 - 91. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Feladat
Hivatkozás(ok):	Feladatok: 1951/március: 267. matematika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Kíséreljük meg a kérdéses szögek cotangenseinek szemléltetését, e célból húzzunk a $B$ és $C$ pontokon át az $A E$ súlyvonallal párhuzamos egyeneseket, majd $A$ -n és $E$ -n át ezekre merőlegest, így egy téglalap keletkezik. ( 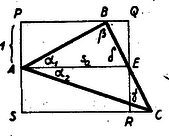$P Q R S$ )

Válasszuk mértékegységül az

A P = A S

távolságot, ekkor

cotg α_{1}

-et

P B

méri, hasonlóképpen

cotg α_{2} = S C

mértékszáma és

cotg δ = B Q = R C

.
Eszerint a bizonyítandó összefüggés

\begin{matrix} S C - P B = 2 Q B, \end{matrix}

amit az ábrából közvetlenül leolvashatunk.

Megoldotta: Durst E.

II. megoldás: Jelöljük az

A B C ▵

szögeit a szokásos módon és fejezzük ki ezeket a bizonyítandó tételben szereplő szögekkel:

\begin{matrix} β = 180^{\circ} - (δ + α_{1}) \\ γ = δ - α_{2} & (1) \end{matrix}

Alkalmazzuk a sinustételt mind az

A C E

, mind az

A E B

háromszögben a közös oldalra és a feltétel szerint egyenlő

(B E = E C)

oldalakra.

\begin{matrix} \frac{A E}{E C} = \frac{sin γ}{sin α_{2}} és \frac{E A}{B E} = \frac{sin β}{sin α_{1}} . \end{matrix}

Az egyenletek baloldalai egyenlők, tehát jobboldalaik is:

\begin{matrix} \frac{sin γ}{sin α_{2}} = \frac{sin β}{sin α_{1}}, \end{matrix}

és beírva és

β

és

γ

(1) alatt kifejezett értékeit

\begin{matrix} \frac{sin (δ - α_{2})}{sin α_{2}} = \frac{sin [180^{\circ} - (δ + α_{1})]}{sin α_{1}} . \end{matrix}

Vegyük figyelembe, hogy

sin [180^{\circ} - (δ + α_{1})] = sin (δ + α_{1})

és alkalmazzuk a szögek összege ill. különbsége sinusának ismert kifejezését:

\begin{matrix} \frac{sin δ cos α_{2} - cos δ sin α_{2}}{sin α_{2}} = \frac{sin δ cos α_{1} + cos δ sin α_{1}}{sin α_{1}} . \end{matrix}

Az osztásokat tagonként elvégezve

\begin{matrix} sin δ cotg α_{2} - cos δ = sin δ cotg α_{1} + cos δ . \end{matrix}

Innen egyszerű átrendezéssel nyerjük a bizonyítandó állítást.

Megoldotta: Béres A., Dávid P., Kántor S. Lipák J., Osztein P., Seitz K., Villányi O., Viski Mária, 2 Névtelen.

Koordinátageometria felhasználásával oldotta meg: Sajó I.