Feladat:	1996. évi Kürschák matematikaverseny 1. feladata	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1997/február, 66 - 68. oldal		PDF  |  MathML
Témakör(ök):	Trapézok, Pitagorasz-tétel alkalmazásai, Háromszög-egyenlőtlenség alkalmazásai, Háromszögek hasonlósága, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):	Feladatok: 1997/február: 1996. évi Kürschák matematikaverseny 1. feladata

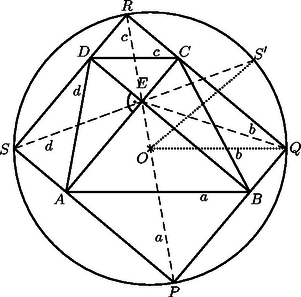
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Jelöljük az átlók metszéspontját $E$-vel, az $AB$, $BC$, $CD$, $DA$, $AE$, $EC$, $BE$, $ED$ szakaszok hosszát rendre $a$, $b$, $c$, $d$, $e_1$, $e_2$, $f_1$, $f_2$-vel (1. ábra). Ekkor azt kell igazolnunk, hogy $bd\ge ac$. Mivel minden tényező pozitív, azért ez egyenértékű annak igazolásával, hogy $b^2{d}^2\ge a^2{c}^2$. Mindegyik tényező egy-egy derékszögű háromszög átfogója. Ezeket Pitagorasz tétele alapján kifejezve az $\begin{array}{c}{\displaystyle \left(e_2^2+f_1^2\right)\left(e_1^2+f_2^2\right)\ge \left(e_1^2+f_1^2\right)\left(e_2^2+f_2^2\right)}\end{array}$ egyenlőtlenséget kell igazolnunk, vagy átrendezve a következőt: $\begin{array}{c}{\displaystyle \left(e_1^2-e_2^2\right)\left(f_1^2-f_2^2\right)\ge 0.}\end{array}$ Ez viszont igaz, mert az $AEB$ és a $CED$ háromszögek hasonlók, így $\begin{array}{c}{\displaystyle e_1\ge e_2\text{és}{f}_1\ge f_2\text{vagy}{e}_1\le e_2\text{és}{f}_1\le f_2\mathrm{.}}\end{array}$ Egyenlőség akkor áll fenn, ha a két háromszög egybevágó, azaz az átlók felezik egymást, tehát a trapéz paralelogramma, mivel pedig az átlói merőlegesek, így rombusz. Ekkor az oldalak egyenlők, s így a két szorzat valóban egyenlő.   II. megoldás. Ismeretes ‐ és a Pitagorasz-tétel négyszeri alkalmazásával könnyen belátható ‐ hogy egy négyszög átlói akkor és csak akkor merőlegesek, ha a szemközti oldalpárok négyzetének az összege egyenlő. Az előző megoldás jelöléseit használva fennáll tehát a következő egyenlőség: $\begin{array}{c}{\displaystyle b^2+d^2=a^2+c^2\mathrm{.}}\end{array}$ Átrendezve és teljes négyzetté kiegészítve ebből az $\begin{array}{c}{\displaystyle {\left(b+d\right)}^2-{\left(a+c\right)}^2=2\left(db-ac\right)}\end{array}$ (1) egyenlőség adódik. Azt kell tehát megmutatnunk, hogy a bal oldal nemnegatív. Ehhez kiegészítjük az ábrát. Hosszabbítsuk meg a $BA$ oldalt $A$-n túl az $AF=c$ szakasszal, továbbá jelöljük $C$ tükörképét $E$-re $G$-vel (2. ábra). Ekkor $ACDF$ paralelogramma, a $BCDG$ deltoidban pedig $BG=b$ és $GD=c$. Így $AGDF$ szimmetrikus trapéz, tehát $GF=d$. A $BGF$ háromszögből a háromszögegyenlőtlenség szerint $\begin{array}{c}{\displaystyle b+d\ge a+c\mathrm{,}}\end{array}$ tehát (1) bal oldala valóban nemnegatív. Egyenlőség akkor áll fenn, ha $G$ $A$-ba esik, vagyis a trapéz átlói felezik egymást, továbbá feltétel szerint merőlegesek, tehát a négyszög rombusz.   III. megoldás. Húzzunk párhuzamosokat a trapéz csúcsain át az átlókkal. Ezek egy $PQRS$ téglalapot határolnak, amit az átlók résztéglalapokra osztanak, így $PE=a$, $QE=b$, $RE=c$, $SE=d$ (3. ábra). Az $ABE$ és $CDE$ háromszögek hasonlók, így az $APBE$ és a $CRDE$ téglalapok is, tehát a $PE$ és az $ER$ átló egy egyenesbe esik, együtt a nagy téglalap átlóját alkotják.   Az ábrán $ac$ eszerint úgy jelenik meg, mint a téglalap köré írt kör átmérője két szeletének szorzata. Messe $SE$ a kört másodszor az $S\text{'}$ pontban. Tudjuk, hogy ekkor $\begin{array}{c}{\displaystyle ac=SE\cdot ES\text{'}=d\cdot ES\text{'}\mathrm{.}}\end{array}$ Azt kell tehát belátnunk, hogy $ES\text{'}\le b$. Feltehetjük, hogy $a\ge c$. Ekkor a kör $O$ középpontja a $PE$ szakaszra esik. A $QOS\text{'}$ háromszög egyenlő szárú. Alapjának a felező merőlegese $O$-n megy keresztül, tehát az $OR$ szakaszra eső $E$ pontra $\begin{array}{c}{\displaystyle ES\text{'}\le EQ=b\mathrm{,}}\end{array}$ és ezt kellett belátnunk. Ismét látható, hogy akkor áll fenn egyenlőség, ha $O$ és $E$ egybeesik, amikor is a trapéz rombusz.