Feladat: 1995. évi Kürschák matematikaverseny 3. feladata Korcsoport: 18- Nehézségi fok: nehéz
Füzet: 1996/február, 69 - 72. oldal  PDF  |  MathML 
Témakör(ök): Vektorok skaláris szorzata, Projektív geometria, Menelaosz-tétel, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):Feladatok: 1996/február: 1995. évi Kürschák matematikaverseny 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A pontokat A-ból hozzájuk mutató helyvektoraikkal jellemezzük. AB→=b, AD→=d. Ezek nem párhuzamosak, tehát a sík vektorai felírhatók egyértelműen ezek számszorosainak összegeként. Így

AC→=c=βb+δd
alkalmas β, δ számokkal.
Mivel E az AB és a CD egyenesen van, F az AD és a BC egyenesen, így
e=AE→=εb=λd+(1-λ)c=(1-λ)βb+((1-λ)δ+λ)d,f=AF→=φd=μb+(1-μ)c=((1-μ)β+μ)b+(1-μ)δd.
Itt λ és μ nem lehet sem 0 sem 1, mert E különbözik C-től és D-től, F pedig B-től és C-től, különben A, C és D, illetőleg A, B és C egy egyenesen volna. Az előállítások egyértelműségéből következik, hogy
ε=(1-λ)β,δ=λλ-1,φ=(1-μ)δ,β=μμ-1,
amiből
ε=(1-λ)μμ-1,φ=λ(1-μ)λ-1.
Ezeket felhasználva
c=μμ-1b+λλ-1d,e=(1-λ)μμ-1b,f=λ(1-μ)λ-1d.(1)

Egy p helyvektorú P pont akkor van az egyes körökön, ha a belőle a megfelelő átmérő végpontjaihoz mutató vektorok merőlegesek, azaz 0 a skaláris szorzatuk3. A feladatban szereplő körök ezért így jellemezhető
p(p-c)=p2-μμ-1pb-λλ-1pd=0,(p-b)(p-d)=p2-pb-pd+bd=0,(p-e)(p-f)=p2-(1-λ)μμ-1pb-λ(1-μ)λ-1pd+λμbd=0.

Jelöljük a bal oldalakat KAC, KBD, KEF-fel. A feladatot megoldottuk, ha sikerül olyan 0-tól különböző α, γ, η számokat találnunk, amelyekre azonosan teljesül, hogy
αKAC+γKBD+ηKEF=0,(2)
mert ekkor, ha egy P pontra valamelyik két kifejezés 0, akkor a harmadik is, tehát ha P valamelyik két körön rajta van, akkor a harmadikon is.
KAC-ben nem szerepel bd-s tag, így bármi is az α, a második kifejezés λμ-szöröséhez a harmadik -1-szeresét adva az összegben ilyen tag nem fog szerepelni. Az összeghez az első kifejezés (1-λμ)-szörösét adva p2 sem fog szerepelni az összegben. Tehát az α=1-λμ, γ=λμ, η=-1 választással a p2-es és a bd-s tagok kiesnek, továbbá a -bp és a -dp együtthatója (2) bal oldalán
(1-λμ)μμ-1+λμ-(1-λ)μμ-1=μμ-1(1-λμ+λ(μ-1)-1+λ)=0;
illetőleg
(1-λμ)λλ-1+λμ-(1-μ)λλ-1=λλ-1(1-λμ+μ(λ-1)-1+μ)=0.

KAC szorzója, α=0 lehetne, ha λμ=1 volna, de ez sem lehetséges. Ha ugyanis ez állna fenn, akkor c (1)-beli előállításában a második törtet λ-val egyszerűsítve azt kapnánk, hogy
c=μμ-1b+11-μdvagyd=μb+(1-μ)c).
Ez azt jelentené, hogy D egybeesnék E-vel, és így egy egyenesen lenne B-vel és C-vel a feladat feltételével ellentétben. Ezzel a feladat állítást bebizonyítottuk.
 
Megjegyzések. 1. A feladatot vektorszámítással megoldó versenyzők többnyire azt számolták ki, hogy ha egy P pontra két egyenlet teljesül, akkor a harmadik is. Ekkor vagy három esetet kell külön-külön végigszámolni, vagy az igényel külön magyarázatot, hogy miért szimmetrikus a három kör szerepe.
2. A feladat megoldható projektív geometriai ismeretek alapján is4. Egy ilyen megoldásnak csak röviden vázoljuk a menetét. Ha R, S, T, U egy egyenes négy különböző pontja, akkor az RT/TS arányt, ezt pozitívnak tekintve, ha a két szakasz egyirányú, negatívnak, ha ellentétes irányú, a három pont osztóviszonyának nevezzük, és (RST)-vel jelöljük. Az (RST)/(RSU) arány a négy pont kettősviszonya, jelölése (RSTU). Ez akkor negatív, ha az R, S és a T, U pontpár elválasztja egymást.
Ha a kettősviszony értéke -1, akkor azt mondjuk, hogy a négy pont harmonikus pontnégyes, illetőleg R, S és T, U harmonikusan választja el egymást5.
A feladat betűzését használva jelöljük a BD és EF, EF és AC, illetőleg AC és BD metszéspontját rendre X, Y, Z-vel, ha létrejönnek (5. ábra). Ekkor A, C és Z, Y, továbbá D, B és X, Z, végül E, F és Y, X harmonikusan választja el egymást. Ha például BEFD trapéz, akkor C felezi a rajta át a párhuzamos oldalakkal párhuzamosan húzott egyenesnek a trapézba eső szakaszát, és így AC felezi a párhuzamos oldalakkal párhuzamosan húzott minden egyenesnek az AB és AD közé eső szakaszát, tehát BD-t és EF-et is6 (6. ábra). Ezekből következik, hogy pl. az AC átmérőjű körben AZ/AY=CZ/CY, s így a kör az ehhez az arányhoz tartozó Apollóniosz-kör7.
Ezután az XYZ háromszög oldalait a C, D, E pontokban metsző egyenesre Menelaos tételét alkalmazzuk8. Eszerint, a háromszög oldalegyeneseit a háromszög valamelyik irányú körbejárása szerint irányítva
(YZC)(ZXD)(XYE)=-1.
Ebből az adódik, hogy ha két kör metszi egymást, akkor a rájuk vonatkozó távolságarányok szorzata a harmadik körre vontkozó arányt adja, vagyis a metszésponton a harmadik kör is átmegy.
Ha pl. EF és BD párhuzamos, akkor Y az EF felezőpontja, Z a BD szakaszé, és hasonló háromszögek felhasználásával fejezhető be az előzőhöz hasonlóan a bizonyítás.
3. A feladat állítását tartalmazza H. S. M. Coxeter, S. L. Greitzer Az újra felfedezett geometria címen megjelent könyvének 2.4.7 tétele9.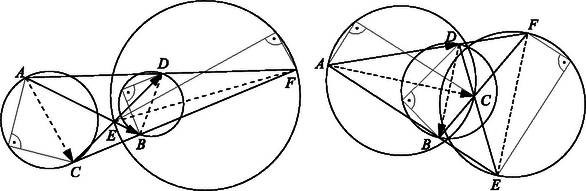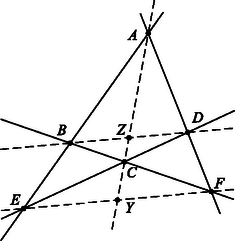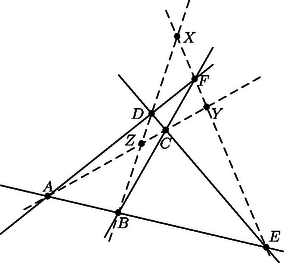
 

 

 
3Vektorokra vonatkozóan lásd pl. Hajós Gy., Neukomm Gy,. Surányi J.: Matematikai Versenytételek II. rész (Tankönyvkiadó, Budapest, 1988) 37‐47. old.; különösen e) pont, 43‐44. old.

4A bizonyítás nélkül felhasználandó ismeretekre vonatkozóan Hajós Gy. Bevezetés a geometriába c. könyvére fogunk utalni (Tankönyvkiadó, Budapest, 1960). A projektív geometria egy minimális feltételekre alapozott (a távolság, szög, folytonosság fogalmát nem használó) felépítésére vonatkozóan lásd pl. a következő művet: H. S. M. Coxeter: Projektvív geometria, Gondolat, Budapest, 1986.

5Hajós idézett műve (a továbbiakban I. m.) 460. old.

6I. m. 462‐463. old.

7I. m. 124. old.

8I. m. 357. old.

9Gondolat Kiadó, 1977., 70. old.