A bizonyításhoz előrebocsátunk két észrevételt.
1. Egy rácsháromszög területének kétszerese, például a koordinátageometria területképletéből láthatóan, egész szám. Így az $1/2$ területű rácsháromszögek nem tartalmaznak rácspontot a belsejükben, de a csúcsaikon kívül a határukon sem ‐ azt fogjuk mondani, üresek ‐ hiszen különben fel lehetne bontani őket három, illetőleg két rácsháromszögre, s így kétszeres területük 1-nél nagyobb volna.¹
2. Az $1/2$ területű derékszögű rácsháromszögek befogóinak a hossza $1$, és a befogók párhuzamosak a koordinátatengelyekkel, mert egyrészt a szorzatuk a háromszög kétszeres területét adja, másrészt két rácspont távolsága nagyobb mint $1$, kivéve, ha egyik koordinátájuk megegyezik, a másik pedig 1-gyel különbözik. Ez azonnal következik a Pitagorasz-tételből.
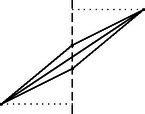
A feladat állításának bizonyításához először egyes háromszögeket kisebb kerületűvel helyettesítünk, de úgy, hogy fél négyzet ($1/2$ területű derékszögű rácsháromszög) ne keletkezzék. Ehhez azt vegyük észre, hogy ha két közös oldalú, üres rácsháromszög együtt konvex négyszöget alkot, akkor ez paralelogramma (1. ábra). Valóban, az ilyen négyszög területe $1/2+1/2=1$, mindkét átló két ‐ legalább, tehát pontosan $1/2$ területű rácsháromszögre bontja, területét felezi, ami azt jelenti, hogy a négyszög paralelogramma. Ha ennek az átlói egyenlők volnának, akkor a négyszög téglalap volna. Így az eredeti két háromszög, mivel területük $1/2$, fél négyzet. A fél négyzeteket azonban nem változtatjuk meg.
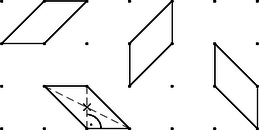
Nem változtatjuk meg azokat a háromszögeket sem, amelyekből a leírt módon két fél négyzet keletkeznék, vagyis a keletkező paralelogramma rövidebb átlója merőleges az egyik párhuzamos oldalpárra. Az ilyen paralelogramma keletkeztethető egy fél négyzetből úgy, hogy azt az egyik befogó középpontjára tükrözzük (2. ábra). Ekkor a hosszabb átló hossza $\sqrt[]{5}$. Nevezzük a továbbiakban az ilyen paralelogrammákat rövidnek.
Ha van a háromszögoldalak közt $\sqrt[]{5}$-nél hosszabb, akkor egy maximális hosszúságú oldalra támaszkodó két háromszögre alkalmazhatjuk a leírt eljárást, mert a háromszögekben ezen az oldalon hegyesszög van, mivel a legnagyobb szög a legnagyobb oldallal van szemben. Így a két háromszög együtt konvex négyszöget alkot. Mivel az előforduló legnagyobb rácstávolságból indultunk ki, és a két átló nem egyenlő hosszú, így a másik átló meghúzásával kisebb kerületű háromszögeket kapunk.
Az eljárás véges sok lépésben befejeződik, mert az oldalhosszak négyzete pozitív egész szám, és nem nagyobb a téglalap átlójánál, továbbá mindegyik csak véges sokszor léphet fel. Elég tehát a feladat állítását olyan téglalapokra belátni, amelyek fél négyzetekre és rövid paralelogrammákra vannak felbontva.
Vegyük a téglalap egyik oldalának két szomszédos rácspont közti szakaszát és a felbontásnak azt a sokszögét, amelyiknek ez az egyik oldala. Ha ez háromszög, akkor megállunk, ha rövid paralelogramma, akkor ennek a tengellyel párhuzamos másik oldalára támaszkodó sokszöget vesszük. Az eljárást addig folytatjuk, amig háromszöghöz vagy a téglalapnak a kiindulási oldalával szemközti oldalához nem érünk. Az első esetben a háromszög egyik befogója a téglalap kiindulási oldalával párhuzamos, így a háromszögnek nem lehet közös oldala a téglalap párhuzamos oldalával.
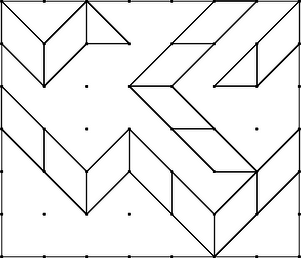
A második esetben a téglalapnak a kiindulási oldallal szomszédos oldalától indulva ki egy egységnyi szakaszból ugyanez az eset csak úgy léphetne fel, ha a két sokszögsorozatnak volna közös rövid paralelogrammája. Ez azonban nem lehetséges, mert az egyik és a másik sorozat rövid paralelogrammáinak a koordinátatengellyel párhuzamos oldala egymásra merőleges (3. ábra).
A leírt eljárás tehát minden esetben legalább kétszer annyi derékszögű üres rácsháromszöget szolgáltat, mint a téglalap valamelyik oldalának a hossza. Ezzel a feladat állítását bebizonyítottuk.