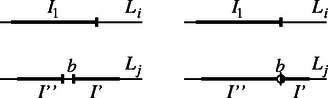|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A következő állítást fogjuk bizonyítani:
Ha az , , , halmaz mindegyike a számegyenes legalább (de véges számú) páronként közös elem nélküli intervallumából áll, akkor kiválasztható mindegyik halmazból egy-egy intervallum úgy, hogy semelyik kettőnek ne legyen közös pontja.
Ez tartalmazza a feladat állítását. Ehhez csak és esetén a , , , halmazokra kell alkalmazni a kimondott tételt.
Az állítás igaz, ha . Ha , eljárást adunk meg az intervallumok egymás utáni kiválasztására. Vegyük mindegyik halmaz balról első intervallumának a jobb végpontját és azt vagy azokat az intervallumokat, amelyekre ez a legkisebb. Több intervallum esetén válasszunk ki egy jobbról nyitottat, ha van ilyen, különben tetszés szerint egyet. Legyen ez , és tartozzék az halmazhoz. Ezután hagyjuk el -t, a többi halmazból pedig a balról első intervallumot, majd ismételjük az eljárást, amíg el nem fogynak a halmazok.
Az első lépés után halmaz marad, mindegyik legalább páronként közös pont nélküli intervallumból áll. Azt kell még belátnunk, hogy -nek a megmaradt intervallumok egyikével sincs közös pontja. Ezzel egyenértékű az, hogy ha -nek az eredeti halmaz intervallumával van közös pontja, ahol , akkor az balról első intervalluma.
Jelöljük bal végpontját -vel, és tegyük fel, hogy van -ben egy -től balra levő intervallum. Ha kisebb jobb végpontjánál, akkor ez még inkább igaz jobb végpontjára (8.a ábra; a halmazokat párhuzamosan eltolt egyeneseken szemléltetjük), így nem -et kellett volna kiválasztanunk.
Ha egyenlő jobb végpontjával, akkor kell, hogy balról, jobbról zárt legyen. Ekkor jobb végpontja vagy kisebb -nél, vagy egyenlő vele, de az utóbbi esetben az intervallum nyitott, mert nincs közös pontja -vel (8.b ábra). Ismét egyik esetben sem -et kellett volna kiválasztani eljárásunk szerint. Ezzel bebizonyítottuk az állítást.
Ezek alapján az eljárást -szer megismételve az összes követelményt kielégítő intervallumhalmazt kapunk.
Megjegyzés. Többen tettek kísérletet annak bizonyítására, hogy a feladat állításában az korlát nem javítható, de ezek hibásak. Az élességét csupán -ra sikerült eddig belátni. Annyit azonban meg lehet mutatni, hogy van olyan halmazrendszer, amelyikből csak -nél kevesebb intervallum választható ki a feladat követelményeinek megfelelően.
Álljon , 2, , -re a | |
nyitott intervallumokból. Legyen a kívánalmaknak megfelelően kiválasztható intervallumok maximális száma . A kiválasztott intervallumok hosszának az összege nem lehet 1-nél nagyobb. Ha minden lépésben kiválaszthatunk egyet a megmaradt legrövidebb intervallumok közül, ez az összeg akkor is legalább | |
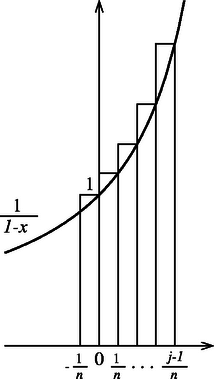
Integrálva -et -től -ig, tekinthető az integrál egy felső közelítő összegének (9. ábra), s így az integrálnak 1-nél kisebbnek kell lennie, azaz | |
Ez tehát felső korlát a kiválasztható intervallumok számára. A nyert konstans:
A megjegyzés Surányi Lászlótól származik.
|
 PDF |
PDF |  MathML
MathML