|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A feladat állításainak bizonyításához előrebocsátunk néhány megjegyzést. Világos, hogy egy konvex sokszögben addig húzhatunk meg egymást nem metsző átlókat, amíg a sokszöget csupa háromszögre nem bontjuk. (A közös végpontokat a következőkben nem tekintjük metszéspontnak.)
Ismeretes, hogy bárhogyan történik ez a felbontás, konvex -szögben ehhez átló szükséges, és azok háromszöget hoznak létre. (Lásd pl. Matematikai Versenytételek III., 1985. évi 1. feladat 2. megjegyzés, 295. oldal.)
A feladat két állítás bizonyítását kívánja. Az elsőt teljes indukcióval bizonyítjuk.
Nyilvánvaló az állítás helyessége háromszögekre ( átló elhagyása után meghúzható egymást nem metsző átló), és négyszögekre is. Legyen a továbbiakban , egy konvex -szög , és tegyük fel, hogy konvex -szögekre igaz az állítás. Legyen az -szögben elhagyva tetszés szerint átló.
Nézzük a második szomszéd csúcsokat összekötő átlókat, nevezzük ezeket a továbbiakban kis átlóknak. Mivel , minden kis átlóhoz egyértelműen tartozik a végpontjai közti, azaz a kis átló által lemetszett csúcs. A kis átlók száma tehát , s így nincs mindegyik elhagyva. Van köztük olyan, amelyik nincs elhagyva, de az általa levágott csúcsból induló átlók közt van elhagyott. Ez nyilvánvaló, ha az elhagyott átlók közt nincs kis átló.
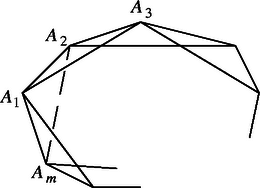
Ha nem ez a helyzet, akkor pl. , , , , sorrendben végighaladva a kis átlókon találunk el nem hagyottat, amire következő el van hagyva. Válasszuk a számozást úgy, hogy nincs elhagyva, el van hagyva. Ekkor az konvex -szög átlói az eredeti sokszögben is átlók, és közülük legfeljebb van elhagyva, mert az elhagyott átló az -szög átlói közt nem szerepel (4. ábra). Így az -szögben meghúzható egymást nem metsző átló az el nem hagyottak közül. Az -szögben ezekhez hozzávehetjük az átlót, mert ez az -szögnek oldala, így egyrészt nincs a meghúzott átlók között, másrészt nem metszi azokat. Az állítás helyessége tehát öröklődik az -szögre is, így minden konvex sokszögre igaz.
A második állítás igazolására megadunk egy konvex -szögben átlót úgy, hogy azok elhagyása után ne lehessen a maradók közül nem metszőt kiválasztani. Erre több lehetőség is kínálkozik.
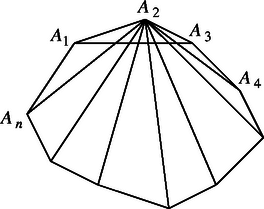
1. Hagyjuk el az -ből induló átlókat és -at (5. ábra). A maradó átlók éppen az -szög átlói. Ezek közül kellene egymást nem metszőt kiválasztani. Láttuk azonban, hogy ebből csak nem metsző átló választható ki. Ezzel igazoltuk a második állítást.
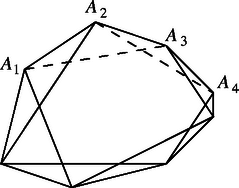
2. A második állítás igazolására alkalmas az is, ha a kis átlókat hagyjuk el az és az kivételével (6. ábra). Ismeretes ugyanis, hogy egy konvex -szögben tetszés szerinti nem metsző átló közt mindig van legalább két kis átló. (A korábban idézett helyen a 3. megjegyzés c) pontja, 295. oldal.) A leírt elhagyás mellett azonban csak két meghúzható kis átló van, de azok metszik egymást. Ezzel újabb bizonyítást adtunk a második állításra.
Megjegyzések. 1. A versenyzők a fentiekben idézett segédtételek közül azokat, amelyeket felhasználtak, be is bizonyították.
2. Az első állításnál négyszög esetén bármelyik átlót hagyjuk el, a másikat kell kiválasztanunk. Megadunk -re is átlót úgy, hogy azok elhagyása esetén csak egyféleképpen lehessen nem metsző átlót kiválasztani. Ehhez ötletet ad a 2. állítás igazolására adott 2. ellenpélda és annak igazolása.
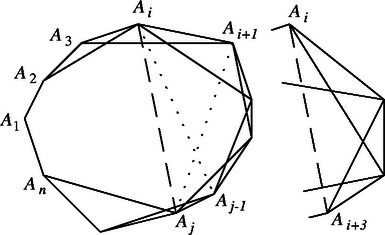
Hagyjuk el az sokszögből a kis átlókat, kivéve az , az és az átlót. Ekkor egyedül az csúcsból induló átlók kiválasztása ad megoldást. Állításunk igazolására megmutatjuk, hogy semelyik átló sem szerepelhet a kiválasztottak közt, ha (7. ábra). Mivel átlóról van szó, és az átló el van hagyva, így legalább 4-oldalú konvex sokszög, és ebben legfeljebb az és kis átló nincs elhagyva, ezek azonban metszik egymást. ( esetén ezek is elhagyott átlók.) Ezzel igazoltuk az állítást.
|
 PDF |
PDF |  MathML
MathML