Feladat:	1994. évi Kürschák matematikaverseny 1. feladata	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1995/február, 67 - 70. oldal		PDF  |  MathML
Témakör(ök):	Pont körre vonatkozó hatványa, Szélsőérték-feladatok, Koszinusztétel alkalmazása, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):	Feladatok: 1995/február: 1994. évi Kürschák matematikaverseny 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Tekintsünk egy $ABCD$ paralelogrammát, amelyikben $AB$ és $BC$ hossza $a$, illetőleg $\lambda a$ ($\lambda >1$), az átlók metszéspontja és a $BC$ oldal felezőpontja $E$, illetőleg $F$. Ekkor $E$ egyben az átlók közös felezőpontja is, így $EF$ az $AB$-vel párhuzamos középvonal fele, hossza $\frac{1}{2}a$. A szóba jövő $E$ pontok tehát az $F$ középpontú, $\frac{1}{2}a$ sugarú $k_E$ kör pontjai, kivéve a $BC$ egyenessel való két metszéspontot, amelyek a kör átellenes pontjai. Szimmetria okokból elég a $BC$ egyenes egyik oldalán levő félkört vizsgálni (1. ábra). A kör átmérője a $BC$ szakasz része. Az átlók szöge a $BC$ szakasz látószöge $E$-ből, tehát tompaszög (hiszen az átmérő látószöge derékszög). Ennek az $\alpha$ szögnek a lehető legkisebb értékét kell tehát meghatároznunk. Belátjuk, hogy $\alpha$ értéke a félkör $E_0$ felezőpontjára a legkisebb. A $BC{E}_0$ háromszög köré írt $k_0$ kört belülről érinti $k_E$, mert mindkét kör középpontja a $BC$-re $F$-ben emelt merőlegesen van, és $k_E$ átmérője a $BC$ szakasz része. A $DE$ és $k_0$ metszéspontját $G$-vel jelölve $\begin{array}{c}{\displaystyle CEB\sphericalangle =CGB\sphericalangle +GCE\sphericalangle >CGB\sphericalangle =C{E}_{0}B\sphericalangle \mathrm{,}}\end{array}$ amint állítottuk. A keresett legnagyobb hegyesszög, ${\phi }_0$ ennek a szögnek mellékszöge, és mivel a $BC{E}_0$ háromszög egyenlő szárú, az $E_{0}BF\sphericalangle$ kétszeresével egyenlő, tehát például így fejezhető ki $\lambda$-val a $B{E}_{0}F$ derékszögű háromszögből: $\begin{array}{c}{\displaystyle \text{<span style="font-weight: normal;font-style: normal;">ctg</span>}\frac{{\phi }_0}{2}=\frac{BF}{E_{0}F}=\frac{\frac{1}{2}\lambda a}{\frac{1}{2}a}=\lambda \mathrm{,}\text{azaz}{\phi }_0=2\text{arc}\text{<span style="font-weight: normal;font-style: normal;">ctg</span>}\lambda \mathrm{,}}\end{array}$ ahol az arkusz-függvény $0^{\circ }$ és ${90}^{\circ }$ közé eső értékét kell venni.   Megjegyzés. A feladat szövege feltételezte ugyan, de meggondolásaink során bizonyítást is nyert, hogy ezt a maximális értéket fel is veszi az átlók szöge, és azt is beláttuk, hogy a téglalapban a legnagyobb ez a szög.   II. megoldás. Válasszuk mértékegységnek az $AB$ oldal hosszát, ekkor $BC$ hossza $\lambda$. Jelöljük az átlók metszéspontját (ami közös felezőpontjuk is) $E$-vel, $AE$ és $EB$ hosszát $e$-vel, illetőleg $f$-fel, a köztük levő szöget $\phi$-vel (2. ábra). A koszinusztételt alkalmazzuk az $AEB$ és a $BEC$ háromszögre. $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle 1}& {\displaystyle =e^2+f^2-2ef\text{cos}\phi \mathrm{,}}\hfill \\ \hfill {\displaystyle {\lambda }^2}& {\displaystyle =e^2+f^2-2ef\text{cos}\left({180}^{\circ }-\phi \right)=e^2+f^2+2ef\text{cos}\phi \mathrm{.}}\hfill \end{array}}}\end{array}$ A megfelelő oldalak összegét és különbségét képezve $\begin{array}{c}{\displaystyle {\lambda }^2+1=2\left(e^2+f^2\right)\mathrm{,}{\lambda }^2-1=4ef\text{cos}\phi \mathrm{.}}\end{array}$ A második egyenlőség bal oldala pozitív, így $\text{cos}\phi$ pozitív, $\phi$ tehát hegyesszög. Alkalmazzuk a második egyenlőségben $e^2$-re és $f^2$-re a mértani és számtani közép közti egyenlőtlenséget, és használjuk fel az első egyenlőtlenséget: $\begin{array}{c}{\displaystyle {\lambda }^2-1\le 4\left(\frac{e^2+f^2}{2}\right)\text{cos}\phi =\left({\lambda }^2+1\right)\text{cos}\phi \mathrm{.}}\end{array}$ Innen $\begin{array}{c}{\displaystyle \text{cos}\phi \ge \frac{{\lambda }^2-1}{{\lambda }^2+1}\mathrm{,}}\end{array}$ és akkor áll fenn egyenlőség, ha $e=f$, azaz ha a paralelogramma téglalap. Mivel a koszinusz-függvény a $\left(0^{\circ };{90}^{\circ }\right)$ számközben a változó csökkenő függvénye, így a keresett legnagyobb ${\phi }_0$ szögre $\begin{array}{c}{\displaystyle \text{cos}{\phi }_0=\frac{{\lambda }^2-1}{{\lambda }^2+1}\mathrm{,}{\phi }_0=\text{arc}\text{cos}\frac{{\lambda }^2-1}{{\lambda }^2+1}\mathrm{,}}\end{array}$ ahol a függvény $0^{\circ }$ és ${90}^{\circ }$ közé eső értékét kell venni.   Megjegyzés. A $\begin{array}{c}{\displaystyle \text{cos}\alpha =\frac{\text{cos}{}^2\left(\alpha /2\right)-\text{sin}{}^2\left(\alpha /2\right)}{\text{cos}{}^2\left(\alpha /2\right)+\text{sin}{}^2\left(\alpha /2\right)}=\frac{\text{<span style="font-weight: normal;font-style: normal;">ctg</span>}{}^2\left(\alpha /2\right)-1}{\text{<span style="font-weight: normal;font-style: normal;">ctg</span>}{}^2\left(\alpha /2\right)+1}}\end{array}$ azonosság alapján világos, hogy az eredmény megegyezik az előző megoldásban nyerttel.   III. megoldás. Az $AC$ átlót rögzítve azok a $D$ pontok, amelyekre az $AD/CD$ arány egy rögzített (1-nél nagyobb) $\lambda$ érték, egy kört alkotnak, az $AC$ szakaszhoz és $\lambda$ arányhoz tartozó Apolloniosz-kört. Jelöljük ezt $k_{\lambda }$-val, $AC$ felezőpontját $E$-vel, $k_{\lambda }$ középpontját $O$-val. Az $AC$ és $ED$ átlók közti szög akkor a legnagyobb, ha $D$ az $E$ pontból a $k$ körhöz húzott érintő $D_0$ érintési pontja. Jelöljük ezt a legnagyobb szöget ${\phi }_0$-val, $k_{\lambda }$-nak az $AC$-re eső átellenes pontjait $P$-vel és $Q$-val, az $AC$ szakasz felét $e$-vel (3. ábra). $P$ és $Q$ ezt a szakaszt belülről, illetőleg kívülről $\lambda :1$ arányban osztó pont, így $\begin{array}{c}{\displaystyle \lambda =\frac{AP}{PC}=\frac{AQ}{QC}\mathrm{.}}\end{array}$ A szereplő szakaszokat $e$-vel fejezve ki a két törtben $\begin{array}{c}{\displaystyle \lambda =\frac{e+EP}{e-EP}=\frac{EQ+e}{EQ-e}\mathrm{.}}\end{array}$ (1) A második egyenlőségből a törtek eltávolítása és rendezés után az $\begin{array}{c}{\displaystyle e^2=EP\cdot EQ}\end{array}$ (2) egyenlőséget kapjuk. (1)-ből $\begin{array}{c}{\displaystyle EP=\frac{\left(\lambda -1\right)e}{\lambda +1}\mathrm{,}EQ=\frac{\left(\lambda +1\right)e}{\lambda -1}\mathrm{.}}\end{array}$ A (2) egyenlőség jobb oldalán álló szorzat az $E$ pontnak a $k_{\lambda }$ körre vonatkozó hatványa, így az egyenlőség azt jelenti, hogy az $E$ pontból a $k_{\lambda }$ körhöz húzott érintő hossza $E{D}_0=e$. A ${\phi }_0$ szög meghatározásakor az $OE{D}_0$ háromszög $O{D}_0$ oldalát, vagyis a $k_{\lambda }$ kör $r$ sugarát fejezzük ki $e$-vel és $\lambda$-val. $\begin{array}{c}{\displaystyle r=\frac{1}{2}PQ=\frac{1}{2}\left(EQ-EP\right)=\frac{1}{2}\left(\frac{\lambda +1}{\lambda -1}-\frac{\lambda -1}{\lambda +1}\right)e=\frac{2\lambda e}{{\lambda }^2-1}\mathrm{.}}\end{array}$ Az $EO{D}_0$ derékszögű háromszögből tehát $\begin{array}{c}{\displaystyle \text{<span style="font-weight: normal;font-style: normal;">tg</span>}{\phi }_0=\frac{r}{e}=\frac{2\lambda }{{\lambda }^2-1}\mathrm{,}{\phi }_0=\text{arc}\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\frac{2\lambda }{{\lambda }^2-1}\mathrm{,}}\end{array}$ ahol a $0^{\circ }$ és ${90}^{\circ }$ közé eső értékeket kell venni.   Megjegyzések. 1. Az előző megoldásokkal való kapcsolat könnyen adódik például a $\begin{array}{c}{\displaystyle \text{<span style="font-weight: normal;font-style: normal;">tg</span>}\alpha =\frac{2\text{<span style="font-weight: normal;font-style: normal;">tg</span>}\frac{\alpha }{2}}{1-\text{<span style="font-weight: normal;font-style: normal;">tg</span>}{}^2\frac{\alpha }{2}}=\frac{2\text{<span style="font-weight: normal;font-style: normal;">ctg</span>}\frac{\alpha }{2}}{\text{<span style="font-weight: normal;font-style: normal;">ctg</span>}{}^2\frac{\alpha }{2}-1}}\end{array}$ összefüggésből.   2. Az $E{D}_0=e$ egyenlőség szerint $D_0$ az $AC$ átmérőjű körön van, így az $AC{D}_0$ háromszög derékszögű, vagyis az a paralelogramma, amelyikre az átlók szöge a legnagyobb, a téglalap.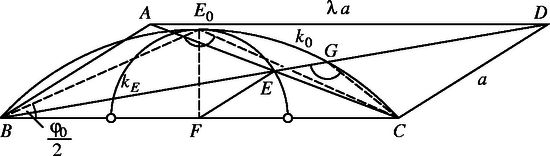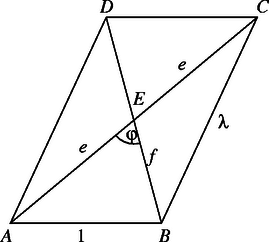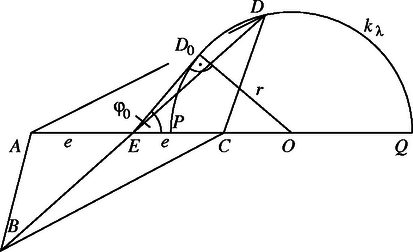