Feladat: 1955. évi Kürschák matematikaverseny 3. feladata Korcsoport: 18- Nehézségi fok: nehéz
Füzet: 1956/február, 38 - 40. oldal  PDF  |  MathML 
Témakör(ök): Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):Feladatok: 1956/január: 1955. évi Kürschák matematikaverseny 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Először belátjuk, hogy ha egy rácspontot egy másik rácspontra, vagy pedig két rácspont összekötő szakaszának felezőpontjára tükrözünk, akkor a tükörkép rácspont. Tudjuk ugyanis, hogy ha az A pontot B-re tükrözve a C ponthoz jutunk, akkor A és C megfelelő koordinátáinak összegei a B pont megfelelő koordinátáinak kétszeresével egyenlők. Két rácspont összekötő szakaszának felezőpontjáról tudjuk tehát, hogy koordinátáinak kétszeresei egész számok. Még inkább igaz ez egy rácspontra, hiszen egész számok kétszeresei is egész számok. Ha most egy rácspontot ilyen pontra tükrözünk, akkor megállapításunk értelmében a tükrözött rácspont és a tükrözéssel nyert pont megfelelő koordinátáinak összegei egész számok. A tükrözéssel kapott pont tehát rácspont, mert koordinátái egész számok különbségei.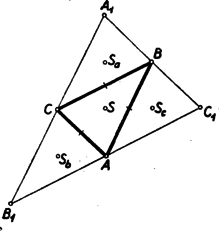
Tekintsük most már a feladatban szerepeltetett ABC háromszöget, s az ennek belsejében levő S rácspontot. Tükrözzük mind e pontokat az ABC▵ oldalainak felezőpontjaira (6. ábra).

 
 
6. ábra
 

Valamennyi kapott pont rácspont. A kapott csatlakozó A1BC, AB1C, ABC1 háromszögek belsejében van rendre az S-ből tükrözéssel nyert Sa, Sb, Sc rácspont. E háromszögek belsejében több rácspont nincs, mert ha pl. az A1BC▵ még egy rácspontot tartalmazna, akkor ezt BC felezőpontjára tükrözve az ABC▵-ön belüli második rácsponthoz jutnánk.
Tükrözzük most az A1 rácspontot Sa-ra. Az így kapott rácspont az A1B1C1 belsejében van, mert az A1 pontból való kétszeres kinagyítás az A1BC▵-et az A1B1C1▵-be, az Sa pontot pedig a szóban forgó rácspontba viszi. Ez a rácspont tehát az S, Sa, Sb, Sc rácspontok valamelyikével azonos, hiszen a fentiek szerint az A1B1C1▵ belsejében nincs más rácspont. Minthogy Sa-ra tükröztünk, Sa maga nem lehet ez a tükörkép. Bizonyítjuk, hogy Sb és Sc sem lehet. Elegendő ezt pl. Sc-re bizonyítanunk. Az AS szakasz tükörképe BC és AB felezőpontjára az A1Sa és BSc szakasz. E szakaszok tehát AS-sel, s így egymással is párhuzamosak és egyenlők. Ezért A1SaSbB paralelogramma, és Sc valóban nem lehet A1-nek Sa-ra vonatkozó tükörképe.
 

Beláttuk így, hogy A1-nek Sa-ra vonatkozó tükörképe csak az S rácspont lehet. Ebből az következik, hogy A1, Sa, S egy egyenesen van. Ez az egyenes áthalad SSa és BC közös felezőpontján, tartalmazza tehát A1-nek e felezőpontra vonatkozó tükörképét, az A pontot is. Eszerint S rajt van az ABC▵ A-ból induló súlyvonalán. Az A, B, C pontok szerepének azonossága miatt rajta van akkor a másik két súlyvonalon is, ezért S az ABC▵ súlypontja.
 

II. megoldás. Felhasználjuk az első megoldás első bekezdésében kimondottakat. Eszerint egy rácspontból való kétszeres kinagyítás minden rácspontot rácspontba visz.
Legyen ismét S a szerepeltetett ABC▵ belsejében levő rácspont. Az S pontnak e háromszög középvonalai által alkotott A'B'C'▵ belsejében kell lennie (7. ábra), mert ha pl. az AB'C'▵ tartalmazná az S pontot, akkor az A pontból való kétszeres kinagyítás S-et az ABC▵ által tartalmazott újabb rácspontba vinné.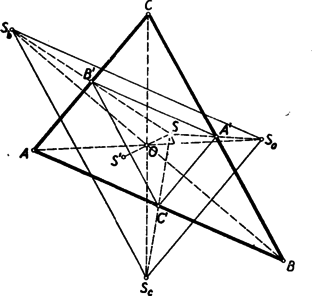
 
 
7. ábra
 

Az S pontot az A', B', C' pontokra tükrözve az Sa, Sb, Sc rácspontokat kapjuk. Az ASa, BSb, CSc szakaszoknak közön O felezőpontjuk van. Ezt pl. az ASa és BSb szakaszokra abból következtetjük, hogy ABSa Sb paralelogramma, hiszen AB és SaSb párhuzamosak és egyenlők, mert mindkettő az A'B' szakasznak (C-ből, ill. S-ből való) kétszeres kinagyításával keletkezik.
Az S pontnak O-ra vonatkozó tükörképe egy S' rácspont. Minthogy S az A'B'C'▵-ben, tehát még inkább az SaSbSc▵ belsejében helyezkedik el, azért S' e háromszög O-ra vonatkozó tükörképében, az ABC▵-ben van. Minthogy azonban ebben a háromszögben csak egyetlen rácspont van, kell, hogy S egybeessék S'-vel, tehát O-val is.
Ezek szerint az AS, BS, CS egyenesek azonosak az SSa, SSb, SSc egyenesekkel, tehát áthaladnak az A', B', C' pontokon. Ezek az egyenesek tehát az ABC súlyvonalai, és S a súlypontja.
 

III. megoldás. Háromszögünket egyik oldalának felezőpontjára tükrözve paralelogrammához jutunk. E paralelogramma belsejében tartalmazza a háromszögünk belsejében levő rácspontot és annak tükörképét, több rácspontot azonban nem. Ezt már az első megoldás bevezető részében is beláttuk. Elég ezért a következő állítást bizonyítanunk.
Ha egy paralelogramma csúcsai rácspontok, a határán több rácspont nincs, és belsejében két rácspont van, akkor ezek a paralelogrammának egy átlóján vannak, s azt harmadolják.
Először azt látjuk be, hogy egy paralelogramma belsejében levő ponthoz mindig található a paralelogrammának olyan csúcsa, hogy az e csúcsból való kétszeres kinagyítás azt a pontot a paralelogrammához tartozó pontba viszi. Ez nyomban következik abból, hogy a paralelogrammát két középvonala négy paralelogrammára bontja, és ezeknek mindegyike egy‐egy csúcsból kétszeresre nagyítva a teljes paralelogrammába megy át. Tekintsük most már az állításunkban szerepeltetett paralelogrammát, és az ennek belsejében elhelyezkedő S és T rácspontokat (8. ábra).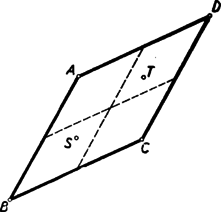
 
 
8. ábra
 

Nem szerepelhet ezek között a paralelogramma középpontja, mert akkor a másiknak erre vonatkozó tükörképe a paralelogramma belsejében elhelyezkedő harmadik rácspontot adna.
Az előre bocsátottak szerint a paralelogramma egyik B csúcsának S-re vonatkozó tükörképe a paralelogrammához tartozik. Ez a tükörkép nem lehet a paralelogrammának csúcsa, mert S nincs a paralelogramma határán és nem azonos a paralelogramma centrumával. Kell tehát, hogy e tükörkép a T pont legyen.
Ugyanígy adódik, hogy egy D csúcsnak T-re vonatkozó tükörképe S-sel azonos. Ezzel beláttuk, hogy S és T harmadolják a BD szakaszt. BD a paralelogrammának csak átlója lehet, hiszen S és T nem lehet a paralelogramma határán. Ezzel állításunkat bizonyítottuk.
 

IV. megoldás. Ismét támaszkodunk az első megoldás első bekezdésében kimondottakra.
A feladatban szereplő ABC▵-et súlyvonalai hat háromszögre bontják (9. ábra).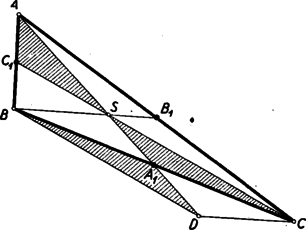
 
 
9. ábra
 

Az ABC▵ belsejében levő egyetlen rácspontot e hat háromszögnek legalább egyike, pl. az AC1S▵ belsejében vagy határán tartalmazza, nem lehet azonban e rácspont az AC1 szakaszon. Az A pontból való kétszeres kinagyítás ezt a rácspontot olyan újabb rácspontba viszi, amelyik az AC1S▵ kinagyításával kapott ABD▵-ben vagy annak határán van, de nincs az AB szakaszon. Minthogy az ABC▵ nem tartalmazhat belsejében második rácspontot, az újabb rácspontnak az A1BD▵-ben vagy annak határán kell lennie, de B-vel azonos nem lehet. Ha most ezt a háromszöget az általa tartalmazott rácsponttal együtt az A1 pontra tükrözzük, azt kapjuk, hogy az A1CS▵-ben vagy annak határán van egy C-től különböző rácspont. Ez a rácspont csak az ABC▵-ben levő egyetlen, AC1S▵ által is tartalmazott rácspont lehet. Ez az egyetlen rácspont azonos tehát háromszögünk S súlypontjával, hiszen az AC1S és A1CS háromszögeknek nincs más közös pontja.
 

Megjegyzés. A harmadik feladat állításának térbeli megfelelője nem igaz: van olyan tetraéder, melynek csúcsai rácspontok, határán nincs több rácspont, és belsejében egyetlen, a tetraéder súlypontjától különböző rácspont van. Így pl. az A(0, 0, 0), B(1, 0, 0), C(0, 1, 0), D(2, 2, 5) csúcsok által adott tetraéder csak az R(1, 1, 2) rácspontot tartalmazza belsejében, és ez a tetraédernek nem súlypontja.