Feladat: 1955. évi Kürschák matematikaverseny 1. feladata Korcsoport: 18- Nehézségi fok: nehéz
Füzet: 1956/február, 33 - 35. oldal  PDF  |  MathML 
Témakör(ök): Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):Feladatok: 1956/január: 1955. évi Kürschák matematikaverseny 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Segédtételként előre bocsátjuk a következő megállapítást: Ha két derékszögű háromszögben az egyik befogó ugyanakkora, és a két háromszög nem egybevágó, akkor ugyanabban a háromszögben található a másik befogóknak és az átfogóknak nagyobbika az egyenlő befogókkal szemközti szögeknek pedig kisebbike. Ennek belátására fektessük egymásra a két háromszöget úgy, hogy derékszögeik és egyenlő befogóik fedjék egymást (1. ábra).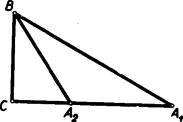

 
 
1. ábra
 

Az egyiknek CA1 befogója túlnyúlik ebben a helyzetben a másiknak CA2 befogóján, hiszen a háromszögek nem egybevágók. A keletkező A1A2B▵ tompaszögű, s ezért BA1>BA2. Ugyanennek a háromszögnek külső szögére vonatkozólag viszont 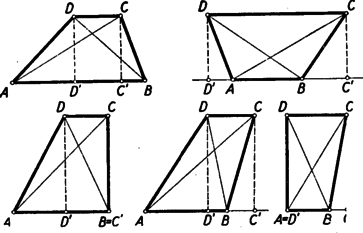BA1C∢<BA2C∢ adódik.
 
 
2. ábra
 

Tekintsük most már az ABCD trapéz AB alapján nyugvó szögeket (2. ábra), és legyen
DAB∢<CBA∢.(1)
A C és D csúcsot az AB egyenesre vetítve a C' és D' pontokhoz jutunk. Bizonyítanunk kell az
AC>BD(2)
egyenlőtlenséget. Elegendő ehhez az
AC'>BD'(3)
egyenlőtlenséget bizonyítanunk. Ha ugyanis BD'≠0, akkor segédtételünket az ACC' és BDD' háromszögekre alkalmazva (3)-ból (2) adódik. Ha viszont B és D' azonos, akkor BD=CC', és így (2) abból adódik, hogy az ACC' derékszögű háromszög átfogója a befogónál hosszabb.
(3) bizonyításánál a DAB és CBA szög minőségének megfelelően három esetet különböztetünk meg.
1. Ha mindkettő hegyesszög, akkor segédtételünket az ADD' és BCC' háromszögekre alkalmazva (1) alapján AD'>BC' adódik, és az ezeket AB-re kiegészítő szakaszokra (3) érvényes. 2. Ha mind a két szög tompaszög, akkor ismét az ADD' és BCC' háromszögekre alkalmazzuk segédtételünket. Most azonban DAD'∢>CBC'∢, mert ezek az (1)-ben szereplő szögeknek kiegészítő szögei. A segédtétel alapján tehát AD'<BC', és ezeket AB-vel megnövelve (3) adódik.
3. Ha DAB∢≤90∘ és CBA∢≥90∘, akkor az AB egyenesen az AB→ irányban haladva D' nem lehet A előtt, és C' nem lehet B előtt. Az AC' szakasz tartalmazza tehát a BD' szakaszt. Ez utóbbi nem lehet AC'-vel azonos sem, mert (1) miatt nem lehet mind a két szereplő szög derékszög. A részként tartalmazott szakasz hosszára tehát teljesül a (3) egyenlőtlenség.
 

II. megoldás. Növeljük meg az ABCD trapéz AB alapján nyugvó kisebbik, DAB∢-ét akkorára, amekkora a CAB∢. Így az egyenlő szárú ABCE trapézhez jutunk (3. ábra), melynek átlói a szimmetria miatt az AB szakasz felezőmerőlegesén metszik egymást.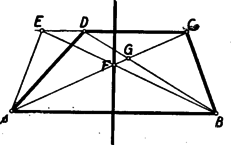
 
 
3. ábra
 

Ezt az F metszéspontot C-vel összekötő FC szakasz a felezőmerőlegesnek azon az oldalán van, amelyiken a B pont. Ugyanezen az oldalon van tehát az eredeti trapéz átlóinak G metszéspontja is, hiszen a D pont az EC szakasz belsejében van, és a BCE▵-ből az adódik, hogy BD metszi az FC szakaszt. Minthogy az AB szakasz felezőmerőlegese által meghatározott félsíkok közül a B pontot tartalmazónak pontjai közelebb vannak B-hez, mint A-hoz, ez áll a G pontra, azaz
GA>GB.
Az ABG▵ és CDG▵ hasonló, mert szögeik páronként csúcsszögek, ill. váltószögek. A bizonyított egyenlőtlenség következményeként tehát
GC>GD.
Egyenlőtlenségeink összegezésével a bizonyítandó AC>BD egyenlőtlenséget kapjuk.
 

III. megoldás. Az ABCD trapéz AB alapján nyugvó kisebbik szög növelésével egyenlő szárú ABCE trapézhez jutunk (4. ábra). E trapéz szimmetria‐tengelye az EC szakasz felezőmerőlegese. Minthogy B ennek a felezőmerőlegesnek azon az oldalán van, amelyiken a felezett CE szakasz C végpontja, azért BC<BE. A szimmetria folytán AC=BE. A BCD és BDE háromszögek D-nél fekvő szögei egymást 180∘-ra egészítik ki, ezért e szögeknek valamelyike vagy hegyesszög vagy tompaszög. Minthogy a tompaszöggel szemben a háromszögnek legnagyobb oldala helyezkedik el, a két háromszögnek valamelyikéből az következik, hogy BD kisebb a BE és BC szakaszok valamelyikénél, tehát kisebb e szakaszok nagyobbikánál, az AC-vel egyenlő BE szakasznál.
 

IV. megoldás. Az ABCD trapézt, az AB átlón nyugvó kisebbik szöget növelve, szimmetrikus ABCE trapézzé egészítjük ki (4. ábra).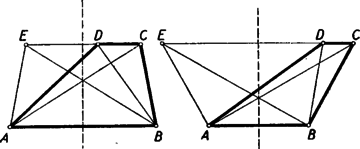
 
 
4. ábra
 

A háromszög külső szögére vonatkozó egyenlőtlenség szerint
EDB∢>DCB∢,
a szimmetria miatt pedig
DCB∢=AED∢.
Így tehát a BDE▵-ben D-nél nagyobb szög helyezkedik el, mint E-nél, mert a BED▵ része az AED∢-nek, amelyről beláttuk, hogy EDB∢-nél kisebb. Minthogy egy háromszögben nagyobb szöggel szemben nagyobb oldal van, így BE>BD. Ezzel a feladat állítását bizonyítottuk, hiszen a szimmetria miatt AC=BE1.
1Ez a megoldás szerepel a Mathematikai versenytételek, I. rész (Középiskolai szakköri Füzetek, Tankönyvkiadó, 1955) 70. oldalán.