Feladat: 1949. évi Kürschák matematikaverseny 2. feladata Korcsoport: 18- Nehézségi fok: nehéz
Füzet: 1951/március, 257 - 258. oldal  PDF  |  MathML 
Témakör(ök): Egyenlő szárú háromszögek geometriája, Középponti és kerületi szögek, Tengelyes tükrözés, Középpontos és egyéb hasonlósági transzformációk, Alakzatok szimmetriái, Pont körre vonatkozó hatványa, Körsorok, Inverzió, Háromszögek hasonlósága, Körülírt kör, Trapézok, Húrnégyszögek, Szimmetrikus alakzatok, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):Feladatok: 1950/március: 1949. évi Kürschák matematikaverseny 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

a) A Kürschák verseny 2. feladata és általánosítása.

 

Lapunk 3. számában a szóbanforgó feladat öt különböző megoldását adtuk és további feladatul tűztük ki e megoldások általánosítását. Mielőtt erre rátérnénk, közöljük a feladatot és egy VI. megoldását, ez is általánosítható.
Egy egyenlőszárú háromszög alapján felvett P pontból a szárakkal párhuzamost húzunk, ezek a szárakat Q és R pontban metszik. Bizonyítandó, hogy a P pontnak a QR egyenesre vonatkozó tükörképe az egyenlőszárú háromszög köré írt kör kerületén van.
 

VI. megoldás: Legyen az egyenlőszárú háromszög ABC, az alapján felvett pont P=A', a feladat szerint a szárakkal húzott párhuzamosokat messük el egy a háromszög alapjával párhuzamos, A-n átfektetett egyenessel is, a metszéspontok legyenek 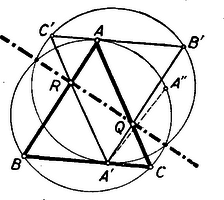C' és B'.
 
 

Nyilván ABC▵≃A'B'C'▵, hiszen A'C'=AC és A'B'=AB, mert egy-egy parallelogrammának szembenfekvő oldalai BAC∢=B'A'C'∢, mint az AQA'R paralelogrammának szembenfekvő szögei. Így az ABC köré írt k kör és az A'B'C' köré írt k' kör egyenlő sugarú és ha ki tudnánk mutatni, hogy QR a két körnek hatványvonala, akkor egyúttal szimmetriatengelyük is volna, ez pedig biztosítaná hogy a k'-n fekvő A' pont tükörképe A'' a k-n legyen. QR azonban valóban a két kör hatványvonala, mert Q-nak is R-nek is egyenlő mindkét körre vonatkozó hatványa: QA⋅QC=QB'⋅QA', mert QA=QB', QC=QA', hasonlóképpen RA⋅RB=RC'⋅RA'.
 

A feladat általánosítása arra az esetre, ha a háromszög nem egyenlőszárú:
Az ABC háromszög BC oldalán felvesszük a P pontot, a PC szakasz felező merőlegese az AC oldalt a Q pontban, a PB szakasz felező merőlegese az AB oldalt az R pontban metszi. A P pontnak a QR egyenesre vonatkozó tükörképe az ABC háromszög köré írt körön van.
Az előbbi módszer erre így vihető át: A feladatban szereplő P pontot jelöljük most is A'-vel. Húzzuk meg A-n át a BC-vel párhuzamos egyenest, ez messe A'Q-t a B', A'R egyenest a C' pontba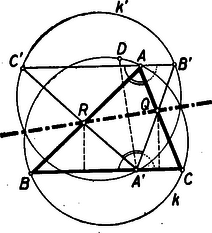n.
 
 

Nyilván ABC▵≃A'B'C'▵ miután A'B' tükörképe CA-nak A'C felező merőlegesére nézve, A'C' tükörképe BA-nak BA' felező merőlegesére nézve és a két ívvel megjelölt A'∢=A∢, mert az azokat 180∘-ra kiegészítő egy ívvel illetve pontozással megjelölt szögek egyenlők. Így az ABC▵ köré írt k kör sugara egyenlő az A'B'C'▵ köré írt k' kör sugarával, QR-ről emiatt ismét elég belátni, hogy a két kör hatványvonala, mert ez esetben szimmetriatengelyük is, tehát a k'-n fekvő A' tükörképe A'' tényleg k-n lenne. Az előbbi esethez hasonlóan, most is egyszerűen beláthatjuk, hogy Q-nak is egyenlő mind a két körre vonatkozó hatványa, R-nek is.