Feladat:	223. fizika feladat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Belényessy István ,  Góth László
Füzet:	1962/szeptember, 42 - 43. oldal		PDF  |  MathML
Témakör(ök):	Kirchhoff II. törvénye (huroktörvény), Ellenállások párhuzamos kapcsolása, Feladat, Egyéb egyenáram
Hivatkozás(ok):	Feladatok: 1962/január: 223. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.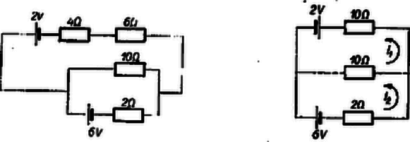     1. ábra   I. megoldás. Vegyük fel az 1. ábra szerint az $I_1$, $I_2$ hurokáramokat, miután a sorbakapcsolt ellenállásokat eredőjükkel helyettesítettük. A feszültségeket V-ban, az ellenállásokat $\Omega$-ban, az áramerősségeket A-ben mérve, Kirchhoff II. törvénye a két hurokra: ${\displaystyle \begin{array}{cc}\hfill {\displaystyle }& {\displaystyle 2=20I_1-10I_2}\hfill \\ \hfill {\displaystyle }& {\displaystyle 6=12I_2-10I_1\mathrm{,}}\hfill \end{array}}$ ahonnan $\begin{array}{c}{\displaystyle I_1=0\mathrm{,}6\text{A, <math xmlns="http://www.w3.org/1998/Math/MathML"><mrow><msub><mrow><mi>I</mi></mrow><mrow><mn>2</mn></mrow></msub></mrow></math>=1}\text{A. }}\end{array}$ A középső ellenálláson 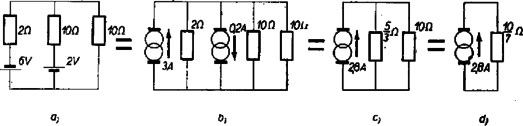$I_2-I_1=0\mathrm{,}4$ A áram folyik $I_2$ irányban.    Belényessy István (Bp., Piarista g. IV. o. t.)   II. megoldás. A 2a ábra szerint fogjuk fel kapcsolásunkat egy három kétpólusból álló lineáris hálózatnak. Vegyük az első kettő Norton ekvivalensét (2b ábra), amihez csupán a forrás‐áramokat kell meghatározni mint az üresjárási feszültség és a belső ellenállás hányadosát: $6\text{V/2 <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>Ω</mi></math>=3 }\text{A}$, $2\text{V/10 <math xmlns="http://www.w3.org/1998/Math/MathML"><mi>Ω</mi></math>=0,2 }\text{A}$. Vegyük ezek eredőjét úgy, hogy a forrásáramokat összeadjuk, az ellenállásokat pedig a párhuzamos kapcsolás szabályainak vetjük alá: $3-0\mathrm{,}2=2\mathrm{,}8\text{A}$, $2\cdot 10/\left(2+10\right)=5/3\Omega$. (2c ábra).     $\begin{array}{c}{\displaystyle \text{<span style="font-style: italic;">2. ábra</span>}}\end{array}$   Végül az 5/3$\Omega$-os és a 10$\Omega$-os ellenállás párhuzamos eredője $\frac{10\cdot 5/3}{10+5/3}=\frac{50}{35}=\frac{10}{7}\Omega$. Eredőképpen a $2\mathrm{,}8$ A-os áramforrás a $10/7\Omega$-os ellenálláson $2\mathrm{,}8\cdot 10/7=4$ V-os feszültséget állít elő. Így a 2a ábrán nézve az első ellenálláson $4-6=-2$ V, a másikon $4+2=6$ V, a harmadikon 4 V esik, tehát az átfolyó áram (felülről lefele) $-1$ A, $0\mathrm{,}6$ A, $0\mathrm{,}4$ A.   Góth László (Bp. Könyves Kálmán g. IV. o. t.)