Kezdőlap


Feladat:	162. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Halasi Pál , Puha Katalin
Füzet:	1961/december, 234 - 235. oldal		PDF \| MathML
Témakör(ök):	Centrifugális erő, Körmozgás (Tömegpont mozgásegyenlete), Egyéb kényszererő, Feladat
Hivatkozás(ok):	Feladatok: 1961/május: 162. fizika feladat

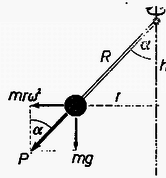
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Először a forgatónyomatékok segítségével vizsgáljuk meg, hogy adatainktól függően milyen helyzetű lesz a (stabilis) egyensúly: a függőlegesből való kitérés $α$ szöge mikor különbözik 0-tól. A centrifugális erő forgatónyomatéka a rúd csuklós forgáspontjára vonatkoztatva tetszőleges $α$ szögnél (e nyomaték ,,kifelé'' forgató irányát tekintsük pozitívnak):

\begin{matrix} F_{1} = h \cdot m r ω^{2} = R sin α \cdot m R ω^{2} cos α . \end{matrix}

A nehézségi erő forgatónyomatéka;

F_{2} = - r \cdot m g = - R sin α \cdot m g

. A kettő eredője:

F = F_{1} + F_{2} = R sin α (m R ω^{2} cos α - m g)

. Tehát, ha

m R ω^{2} \leq m g

F

negatív, ha

α \neq 0

, így egyensúly csak az

α = 0

helyzetben van (

F = 0

), és ez stabilis: más helyzetből

F

ebbe a helyzetbe forgat. Ha

m R ω^{2} > m g

, akkor aszerint, hogy

cos α

nagyobb-e vagy kisebb-e a nem függőleges

F = 0

egyensúlyi helyzetnek megfelelőnél, azaz

α

kisebb-e vagy nagyobb-e ez egyensúlyi kitérésnél,

F

kifelé vagy befelé forgat, tehát ez az egyensúlyi helyzet a stabilis. Az ekkor is meglevő

α = 0

egyensúly nyilván labilis, tehát a gyakorlatban nem állhat fenn. A keresett

P

feszítőerő az első esetben tehát a nehézségi erő. A második esetre az egyensúlyi helyzet valamely adatának az

F = 0

egyenletből való kifejezése útján történő megoldásnál rövidebb a következő:
Az ábrán feltüntetett hasonló háromszögekből

\begin{matrix} R : r = P : m r ω^{2}, így P = m R ω^{2} . \end{matrix}

A számpéldáknál az a) esetben

m R ω^{2} < m g

, így utóbbi képletünk alkalmazható, és

P = 20, 25 newton = 2, 07 kp

, míg b) esetben

m R ω^{2} > m g

, így

P = 1 kp

(a golyó súlya).

Puha Katalin (Győr, Kazinczy g. III. o. t.) és

Halasi Pál (Nagykanizsa, Landler g. III. o. t.) dolgozata alapján