Kezdőlap


Feladat:	149. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Góth László , Puha Katalin , Schaub Zsuzsa , Széchényi K. , Vesztergombi György
Füzet:	1961/november, 180 - 181. oldal		PDF \| MathML
Témakör(ök):	Hajítások, Függőleges hajítás, Tökéletesen rugalmas ütközések, Egyéb mozgás lejtőn, Feladat
Hivatkozás(ok):	Feladatok: 1961/április: 149. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az idézett feladat megoldásának eredménye szerint

\begin{matrix} tg α = 2 tg β + ctg 2 β . \end{matrix}

A kétszeres szögre vonatkozó összefüggések szerint átalakítva:

\begin{matrix} tg α = 2 tg β + \frac{1 - tg^{2} β}{2 tg β} = \frac{1 + 3 tg^{2} β}{2 tg β} . \end{matrix}

(1)

A továbbiakban szükségünk lesz a következő szögfüggvényekre is:

\begin{matrix} cos^{2} α = \frac{1}{1 + tg^{2} α} = \frac{4 tg^{2} β}{1 + 10 tg^{2} β + 9 tg^{4} β} . \end{matrix}

A nevezőt szorzattá alakítjuk:

\begin{matrix} cos^{2} α = \frac{4 tg^{2} β}{(1 + tg^{2} β) (1 + 9 tg^{2} β)} . \end{matrix}

(2)

(1) szerint bármely lejtőhöz található hajítási szög, mert

β

pozitív hegyesszög. A tetőzés mértani helyét rögtön megadhatjuk, hiszen a tetőpontban a sebesség zérus, így az energiamegmaradás elve szerint a kezdeti

m g F

(F = \frac{c^{2}}{2 g})

mozgási energia minden hajításnál azonos lévén, a tetőzések az

y = F

egyenesen vannak.
A becsapódás abszcisszájára az idézett feladat megoldása szerint

\begin{matrix} x = 4 F cos^{2} α (tg α - tg β) = 4 F \frac{4 tg^{2} β}{(1 + tg^{2} β) (1 + 9 tg^{2} β)} \cdot \frac{1 + tg^{2} β}{2 tg β} = 8 F \frac{tg β}{1 + 9 tg^{2} β} . \end{matrix}

Mivel a lejtő egyenlete

tg β = y / x

, ezt behelyettesítve:

\begin{matrix} x = 8 F \frac{\frac{y}{x}}{1 + 9 {(\frac{y}{x})}^{2}} . \end{matrix}

A törteket eltávolítva

\begin{matrix} x^{2} + 9 y^{2} = 8 F y . \end{matrix}

Teljes négyzetté alakítva

\begin{matrix} x^{2} + 9 {(y - \frac{4}{9} F)}^{2} = 9 {(\frac{4}{9} F)}^{2}, \end{matrix}

amely egy ellipszis egyenlete:

\begin{matrix} \frac{x^{2}}{{(\frac{4}{3} F)}^{2}} + \frac{{(y - \frac{4}{9} F)}^{2}}{{(\frac{4}{9} F)}^{2}} = 1, \end{matrix}

A becsapódási pontok mértani helye ezen ellipszisnek az ábrán látható fele.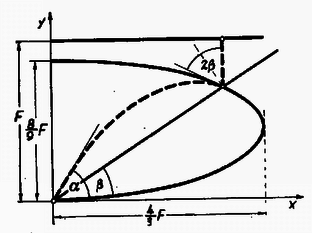

Vesztergombi György (Bp., Piarista g. III. o. t.) dolgozata alapján.