Kezdőlap


Feladat:	137. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Góth László , Simonovits Miklós , Szidarovszky Ágnes , Vesztergombi György
Füzet:	1961/november, 172 - 173. oldal		PDF \| MathML
Témakör(ök):	Egyéb tehetetlenségi nyomaték, Feladat
Hivatkozás(ok):	Feladatok: 1961/március: 137. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Húzzuk meg a háromszög középvonalait, ezek négy darab hozzá hasonló, egybevágó háromszögre bontják.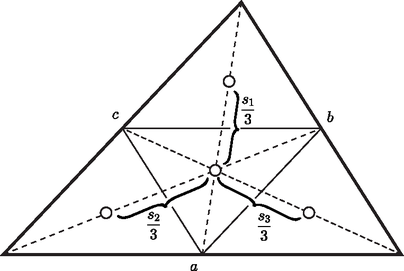

Így a háromszög tömegét

M

-mel jelölve, a kis háromszögek tömege

M / 4

, és súlypontjaik távolsága a nagy háromszög súlypontjától: 0,

s_{1} / 3

s_{2} / 3

s_{3} / 3

. Alkalmazva a XXII. kötet 1. és 2. számában megjelent cikk tételeit:

\begin{matrix} M a_{x}^{2} a^{2} = \frac{M}{4} a_{x}^{2} {(\frac{a}{2})}^{2} + [\frac{M}{4} a_{x}^{2} {(\frac{a}{2})}^{2} + \frac{M}{4} {(\frac{s_{1}}{3})}^{2}] + [\frac{M}{4} a_{x}^{2} {(\frac{a}{2})}^{2} + \frac{M}{4} {(\frac{s_{2}}{3})}^{2}] + [\frac{M}{4} a_{x}^{2} {(\frac{a}{2})}^{2} + \frac{M}{4} {(\frac{s_{3}}{3})}^{2}] \end{matrix}

innen

M

-mel egyszerűsítve, összevonva és rendezve:

\begin{matrix} a_{x}^{2} = \frac{s_{1}^{2} + s_{2}^{2} + s_{3}^{2}}{27 a^{2}} . \end{matrix}

Fejezzük ki a súlyvonalakat az oldalak segítségével! Ismeretes, hogy egy paralelogramma átlóinak négyzetösszege egyenlő oldalainak négyzetösszegével. Alkalmazzuk ezt a nagy háromszögnek oldalfelező pontjaira való tükrözésével nyert paralelogrammákra:

\begin{matrix} 4 s_{1}^{2} + a^{2} = 2 (b^{2} + c^{2}), 4 s_{2}^{2} + b^{2} = 2 (a^{2} + c^{2}), 4 s_{2}^{2} + c^{2} = 2 (a^{2} + b^{2}) . \end{matrix}

Ezen egyenlőségeket összeadva kapjuk, hogy

s_{1}^{2} + s_{2}^{2} + s_{3}^{2} = 3 / 4 (a^{2} + b^{2} + c^{2})

. Tehát a tehetetlenségi nyomaték:

\begin{matrix} Θ = M a_{x}^{2} \cdot a^{2} = \frac{M}{36} (a^{2} + b^{2} + c^{2}) . \end{matrix}

Vesztergombi György (Bp., Piarista g. III. o. t.)

II. megoldás: A keresett tehetetlenségi nyomaték egyenlő a háromszög súlypontján átmenő és az egyik oldallal párhuzamos, valamint a súlyponton átmenő, erre merőleges tengelyekre vonatkozó

Θ_{1}

Θ_{2}

tehetetlenségi nyomatékok összegével. Az előbbi egyenlő egy

l

hosszúságú,

M

tömegű lineárisan növekvő sűrűségű egyenes vonaldarab tehetetlenségi nyomatékával, hiszen a háromszög pontjait eltolhatjuk a tengellyel párhuzamosan.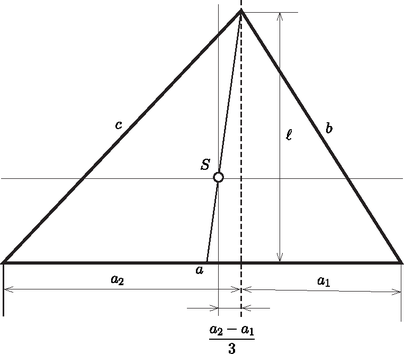

Tehát

Θ_{1} = 1 / 18 M l^{2}

. A második nyomaték meghatározásához előbb kiszámítjuk a háromszög tehetetlenségi nyomatékát az illető tengellyel párhuzamos, harmadik csúcsponton átmenő tengelyre vonatkozólag. A háromszög pontjait ezen tengellyel párhuzamosan eltolva két lineárisan növekvő sűrűségű rudat kapunk; ezek tehetetlenségi nyomatékát kell meghatároznunk a végpontjukon átmenő tengelyre vonatkozólag. A Steiner‐tétel segítségével e két nyomaték összege:

[1 / 18 M_{1} a_{1}^{2} + M_{1} {(a_{1} / 3)}^{2}] + [1 / 18 M_{2} a_{2}^{2} + M_{2} {(a_{2} / 3)}^{2}] = 1 / 6 (M_{1} a_{1}^{2} + M_{2} a_{2}^{2}) = 1 / 6 (M a_{1} / a \cdot a_{1}^{2} + M a_{2} / a \cdot a_{2}^{2}) = 1 / 6 M / a (a_{1}^{3} + a_{2}^{3}) = M / 6 (a_{1}^{2} - a_{1} a_{2} + a_{2}^{2})

. Így a súlyponton átmenő tengelyre vonatkozólag a háromszög tehetetlenségi nyomatéka ugyancsak a Steiner‐tétel alapján

Θ_{2} = M / 6 (a_{1}^{2} - a_{1} a_{2} + a_{2}^{2}) - M {(\frac{a_{2} - a_{1}}{3})}^{2}

. Felhasználva, hogy

l^{2} = b^{2} - a_{1}^{2}

l^{2} = c^{2} - a_{2}^{2}

, a súlyponton átmenő, a háromszög síkjára merőleges tengelyre vonatkoztatott nyomaték:

\begin{matrix} Θ = Θ_{1} + Θ_{2} = 1 / 18 M l^{2} + 1 / 6 M (a_{1}^{2} - a_{1} a_{2} + a_{2}^{2}) - 1 / 9 M (a_{1}^{2} - 2 a_{1} a_{2} + a_{2}^{2}) = \\ = M / 36 (2 l^{2} + 6 a_{1}^{2} - 6 a_{1} a_{2} + 6 a_{2}^{2} - 4 a_{1}^{2} + 8 a_{1} a_{2} - 4 a_{2}^{2}) = \\ = M / 36 (b^{2} - a_{1}^{2} + c^{2} - a_{2}^{2} + 2 a_{1}^{2} + 2 a_{2}^{2} + 2 a_{1} a_{2}) = \\ = M / 36 [b^{2} + c^{2} {(a_{1} + a_{2})}^{2}] = M / 36 (a^{2} + b^{2} + c^{2}) . \end{matrix}

Szidarovszky Ágnes (Bp., Ságvári E. g. III. o.t.)