Kezdőlap


Feladat:	129. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bácsy Zs. , Bollobás Béla , Fritz József , Gál Jenő , Góth László , Kóta József , Náray-Szabó Gábor , Szegő Károly , Székely Jenő
Füzet:	1961/október, 93 - 94. oldal		PDF \| MathML
Témakör(ök):	Tökéletesen rugalmas ütközések, Geometriai szerkesztések alkalmazása, Feladat
Hivatkozás(ok):	Feladatok: 1961/február: 129. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A falon való pattanáskor a labda sebességvektora a beesési merőlegesre tükröződik, iránya ellentétes lesz, ezért a sebesség függőleges komponense változatlan marad, mivel az ütközés függőleges falon történik; a labda vízszintes síkon való vetülete olyan mozgást végez, mintha a fal vetületi egyenesén verődne vissza.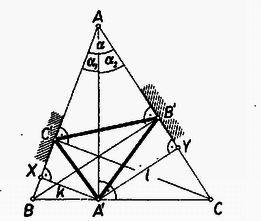
Az $A$ kiindulási pontban az $A A'$ -re állított merőleges messe a falak vetületét a $B$ és $C$ pontban (l. az 1. ábrát).

1. ábra

Ekkor az

A' B' C'

háromszög az

A B C

háromszög talpponti háromszöge, mert két-két oldala

A B

-vel, illetve

A C

-vel ugyanakkora szöget zár be. Így

A B A' B'

húrnégyszög (

B A' A ∢ = B B' A ∢ = 90^{\circ}

). Ebből következik, hogy

B' A' A ∢ = B' B A ∢ = 90^{\circ} - α

, tehát a hajlítás vetülete a vízszintes síkon

A A'

-vel

90^{\circ} - α

szöget zár be. (Ezt az irányt azzal is meghatározhatjuk, hogy

B' A' Y ∢ = α_{1}

, ugyanis

B' A' Y ∢ = A' B' B ∢ = A' A B ∢

‐ váltószögekről, illetve ugyanazon íven nyugvó kerületi szögekről lévén szó.)
Képzeljük a labda mozgását egy síkban ! Mivel ütközéskor a sebesség függőleges komponense változatlan marad, a labda ferde hajítási pályán mozog, melynek teljes útja az

A B C ▵

kerületével egyenlő. Ezt a következőképpen határozhatjuk meg: tükrözzük az

A

pontot az

A B

és

A C

egyenesekre, a nyert tükörpontok távolsága adja meg a háromszög kerületét, az

E F

-nek az

A B

-vel, illetve

A C

-vel alkotott metszéspontja a visszaverődési pontokat.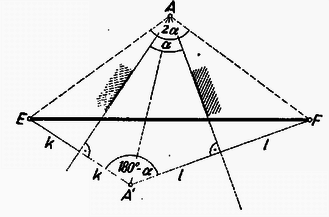

2. ábra

(Ennek alapján a pálya vízszintes síkon való vetülete meg is szerkeszthető. Az is látható, hogy csak

α < 90^{\circ}

esetén van a feladatnak megoldása, hiszen különben

E A F ∢ \geq 180^{\circ}

lenne:

E F

nem metszené a falak vetületét.) Így a

cos

-tétel alapján

\begin{matrix} s = \sqrt[]{{(2 k)}^{2} + {(2 l)}^{2} - 2 \cdot 2 k \cdot 2 l cos (180^{\circ} - α)} = 2 \sqrt[]{k^{2} + l^{2} + 2 k l cos α} . \end{matrix}

A ferde hajítás teljes útja

φ

hajlásszögű

c

kezdősebesség esetén

c^{2} / g sin φ

, így

2 \sqrt[]{k^{2} + l^{2} + 2 k l cos α} = c^{2} / g \cdot sin 2 φ

. Ilyen feltétel mellett az

A B C ▵

kerületével egyenlő vízszintes elmozdulás után a ferdén elhajított test ugyanolyan magasságra jut vissza. Tehát a kezdősebesség nagysága és iránya nincs egyértelműen meghatározva,

c

-nek és

φ

-nek csak a fenti összefüggést kell kielégítenie.

Kóta József (Tatabánya, Árpád g. III. o. t.)

Megjegyzés: A labda vízszintes útját kifejezhetjük az

A A'

távolság segítségével is: az

A E F

egyenlőszárú háromszög szárszöge

2 α

, szárai

A A'

-vel egyenlő hosszúak, így

E F = 2 A A' sin α

Székely Jenő (Pécs, Nagy Lajos g. IV. o. t.)