Kezdőlap


Feladat:	118. fizika feladat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bollobás Béla , Fritz József , Kiss Tünde , Perjés Zoltán , Rába Ferenc , Székács Gy. , Varsányi István
Füzet:	1961/május, 237 - 238. oldal		PDF \| MathML
Témakör(ök):	Súlypont (tömegközéppont) meghatározása, Feladat
Hivatkozás(ok):	Feladatok: 1961/január: 118. fizika feladat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Szeleteljük fel a körkúpot gondolatban a tengelyre merőleges síkokkal, és határozzuk meg a keletkezett körgyűrű idomok súlypontját. Nyilván ezek mind a kúp tengelyén fognak elhelyezkedni.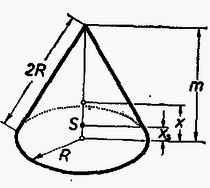

Az egymás után következő csonkakúp palástok felszíne egyenes arányban növekszik, és ezáltal a tengelyre összegezett súlypontok ,,tömege'' is egyenes arányban fog növekedni. Így a tengelyt úgy tekinthetjük, mintha annak súlya lineárisan növekednék. Ha a kúp magasságát, és egyúttal az előbbi tengely hosszát

m

-mel jelöljük, akkor a lap januári számában kidolgozott mintapélda alapján a súlypont helyzetére

x = 1 / 3 m

adódik. Ezzel a palástfelület súlypontját megkaptuk. Jelöljük

R

-rel az alapkör sugarát. A palást felszíne

F_{p} = 2 R^{2} π

, az alaplap területe

F_{a} = R^{2} π

,
Az alaplap súlypontkoordinátája

0

, így a súlypontszámítás ismert képlete szerint a rendszer eredő súlypontkoordinátája:

x_{s} = \frac{F_{p} x}{F_{a} + F_{p}} = \frac{2}{9} m

.
Mivel pedig

m = R \cdot \sqrt[]{3},

x_{s} = R \frac{2 \sqrt[]{3}}{9}

Kiss Tünde (Tamási, Béri Balogh Á. g. III. o. t.)

Megjegyzés: Ha úgy tekintjük, hogy a kúpot egyenletes

d

vastagságú réteg határolja, akkor a súlypont helyzetére természetesen más eredmény adódik. Erre az esetre

\begin{matrix} x_{s} = m - \frac{224 m^{3} - 328 m^{2} m_{1} + 152 m m_{1}^{2} + 5 m_{1}^{3}}{288 m^{2} - 432 m m_{1} + 216 m_{1}^{2}}, \end{matrix}

ahol

m

a magasság:

m = R \cdot \sqrt[]{3}

m_{1} = 2 d

.
Ha felületekre térünk át, akkor a

d = 0

, azaz

m_{1} = 0

értéket helyettesítve természetesen az előbbi

x_{s} = R \frac{2 \sqrt[]{3}}{9}

adódik.

Rába Ferenc (Bp., I. István g. IV. o. t.)